
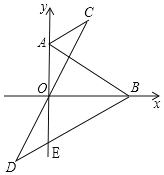
����Ŀ����ƽ��ֱ������ϵ�У���A��0��6����B��8��0����AB=10����ͼ����DBO=��ABO����CAy=��BAO��BD��y���ڵ�E��ֱ��DO��AC�ڵ�C��
��1������֤����ACO�ա�EDO��������߶�AC��BD��λ�ù�ϵ��������ϵ��
��2������P��A��������A��O��B·���˶����ٶ�Ϊ1����B�㴦ֹͣ�˶�������Q��B��������B��O��A�˶����ٶ�Ϊ2����A�㴦ֹͣ�˶�������ͬʱ��ʼ�˶�����Ҫ������Ӧ���յ����ֹͣ����ijʱ�̣���PE��CD�ڵ�E��QF��CD�ڵ�F�����������˶��ʱ��ʱ��OPE���OQFȫ�ȣ�
���𰸡���1��AC��BD��AC=BD��10����2�����������˶�ʱ��Ϊ2��![]() ��12��ʱ����OPE����OQFȫ��.
��12��ʱ����OPE����OQFȫ��.
��������
��1���ٸ���ȫ�������ε��ж�����ASA֤�ý��ۣ�
�����â���ȫ�������ε����ʵõ���AC��BD��AC=BD-10��
��2�����˶���ʱ��Ϊt�룬��i������P��Q�ֱ���y�ᡢx����ʱ��ii������P��Q����y����ʱ����iii������P��x���ϣ�Q��y��ʱ�����߶�û����ǰֹͣ������Q��ǰֹͣʱ���з��̼��ɵõ����ۣ�
��1������ͼ��
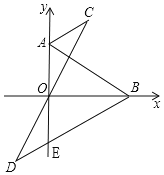
�ߡ�DBO=��ABO��OB��AE��
���BAO=��BEO��
��AB=BE��
��AO=OE��
�ߡ�CAy=��BAO��
���CAy=��BEO��
���DEO=��CAO
����ACO����EDO��
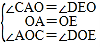 ��
��
���ACO�ա�EDO��ASA����
���ɢ�֪����ACO�ա�EDO��
���C=��D��AC=DE��
��AC��BD��AC=BD��10��
��2�����˶���ʱ��Ϊt�룬
��i������P��Q�ֱ���y�ᡢx����ʱPO=QO�ã�6��t=8��2t�����t=2���룩��
��ii������P��Q����y����ʱPO=QO�ã�6��t=2t��8�����t=![]() ���룩��
���룩��
��iii������P��x���ϣ�Q��y��ʱ�����߶�û����ǰֹͣ����PO=QO�ã�t��6=2t��8�����t=2���룩�������⣻
����Q��ǰֹͣʱ����t��6=6�����t=12���룩��
�������������������˶�ʱ��Ϊ2��![]() ��12��ʱ����OPE����OQFȫ��.
��12��ʱ����OPE����OQFȫ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�м���Ϊ���˽⡰������������Ҫ������������˸��в��������Ե��������������������������в�������ͳ��ͼ����
��� | �۵� | Ƶ���������� |
A | ������ѹ�ͣ����������� | 80 |
B | ����ҳ�����ʪ�ȵ� | m |
C | ����β���ŷ� | n |
D | ������ɵ���Ⱦ | 120 |
E | ���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
��1����գ�m= �� n= ��
��2���������˿�Լ��100���ˣ�����������г�D�顰�۵㡱�����������Ƕ������ˣ�
��3��������ν��ܵ���������У�������һ�ˣ�����˳�C�顰�۵㡱�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2+bx+c��y=x��ͼ����ͼ��ʾ�������½��ۣ� ��b2��4c��0��
��b+c+1=0��
��3b+c+6=0��
�ܵ�1��x��3ʱ��x2+��b��1��x+c��0��
������ȷ�ĸ���Ϊ�� ��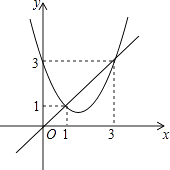
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
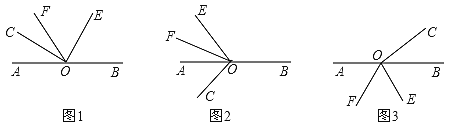
����Ŀ����֪OΪֱ��AB�ϵ�һ��,��COE��ֱ��,OFƽ�֡�AOE(ͼ����˵�ĽǶ���С��ƽ�ǵĽ�).
(1)��ͼ1,����COF=28��,���BOE=______�㣻����COF=![]() ���BOE=_______����BOE���COF��������ϵΪ_________��
���BOE=_______����BOE���COF��������ϵΪ_________��
(2)����COE�Ƶ�O��ʱ����ת����ͼ2��ʾ��λ��ʱ,(1)�С�BOE�͡�COF��������ϵ����Ȼ����������������˵�����ɣ����������������BOE���COF��������ϵ��
(3)����COE�Ƶ�O˳ʱ����ת����ͼ3��λ��ʱ,(1)�С�BOE�͡�COF��������ϵ�Ƿ���Ȼ����?����������˵�����ɣ���������,�������BOE���COF��������ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�
��1���Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ���B��FΪԲ�ģ����� ![]() BF��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
BF��Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��2���ı���ABEF����ѡ����Ρ����Ρ������Ρ���ȷ������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
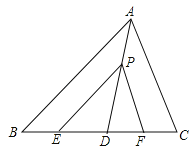
����Ŀ����ͼ���ڡ�ABC�У���D��E��F�ڱ�BC�ϣ���P���߶�AD�ϣ���PE��AB����PFD=��C����D��AB��AC�ľ�����ȣ���֤����D��PE��PF�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲���У��ˮƽ�����ϵ�һ�ô����ĸ߶ȣ���ѧ�ۺ�ʵ���С���ͬѧ�ǿ�չ���»��ijһʱ�̣��������1.6m��С���������µ�Ӱ����1.2m����ͬһʱ�̲����ô�����Ӱ����3.6m��������ĸ߶���m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����DEB�У���֪AB=DE����������������������ʹ��ABC�ա�DEC���������ӵ�һ��������

A��BC=EC����B=��E B��BC=EC��AC=DC
C��BC=DC����A=��D D����B=��E����A=��D
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com