
 如图,已知在△ABC中,D是边BC的中点,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overrightarrow{DA}$等于( )
如图,已知在△ABC中,D是边BC的中点,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overrightarrow{DA}$等于( )| A. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ | C. | $\frac{1}{2}\overrightarrow b-\overrightarrow a$ | D. | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ |
分析 首先由在△ABC中,D是边BC的中点,可求得$\overrightarrow{BD}$,然后由三角形法则求得$\overrightarrow{DA}$.
解答 解:∵在△ABC中,D是边BC的中点,
∴$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{b}$,
∴$\overrightarrow{DA}$=$\overrightarrow{BA}$-$\overrightarrow{BD}$=$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$.
故选B.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用是关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条直线相交,组成的图形叫角 | |
| B. | 两条有公共端点的线段组成的图形叫角 | |
| C. | 两条有公共点的射线组成的图形叫角 | |
| D. | 从同一点引出的两条射线组成的图形也是角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△OAB中,BA⊥OA,且OA=BA=4,点P从O点出发,沿OA以每秒1个单位的速度向A点移动,到达A点停止运动,则△OBP面积S与点P的运动时间t之间的函数图象大致是( )
如图,Rt△OAB中,BA⊥OA,且OA=BA=4,点P从O点出发,沿OA以每秒1个单位的速度向A点移动,到达A点停止运动,则△OBP面积S与点P的运动时间t之间的函数图象大致是( )| A. |  | B. | 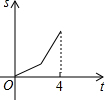 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从OA1B1B2→A2…按此规律,则动点M到达A10点处所需时间为( )秒.
点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从OA1B1B2→A2…按此规律,则动点M到达A10点处所需时间为( )秒.| A. | 10+55π | B. | 20+55π | C. | 10+110π | D. | 20+110π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-2)(m2-m) | B. | m(a-2)(m-1) | C. | m(a-2)(m+1) | D. | m(2-a)(m-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{b}{a}$=$\frac{b+c}{a+c}$ | B. | $\frac{b}{a}$=$\frac{{b}^{2}}{{a}^{2}}$ | C. | $\frac{(x+y)b}{(x+y)a}$=$\frac{b}{a}$ | D. | $\frac{b}{a}$=$\frac{b(x-y)}{a(x-y)}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com