
分析 (1)首先对中括号内的式子用完全平方公式和平方差公式计算,合并同类项,然后利用多项式与单项式除法法则计算,即可化简,然后代入数值计算即可;
(2)首先根据非负数的性质求得x和y的值,然后利用多项式和单项式的除法法则对式子进行化简,最后代入求值即可.
解答 解:(1)原式=[x2-2xy+y2+x2-y2]÷2x
=(2x2-2xy)÷2x
=x-y,
当x=2,y=-1时,原式=2-(-1)=3;
(2)根据题意得:$\left\{\begin{array}{l}{x-3=0}\\{y+2=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,
原式=-3y2-$\frac{1}{4}$xy+2x2,
当x=3,y=-2时,原式=-3×4+$\frac{1}{4}$×3×2+2×9=-12+$\frac{3}{2}$+18=$\frac{15}{2}$.
点评 本题考查了整数的混合运算以及非负数的性质,主要考查了公式法、单项式与多项式相乘以及合并同类项的知识点.


科目:初中数学 来源: 题型:选择题
| A. | 150m | B. | 125m | C. | 120m | D. | 80m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
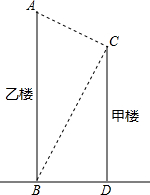 如图,在一幢高CD=15m的甲楼顶端C处,测得乙楼底部B的俯角为63°,乙楼顶端A的仰角为25°.求:
如图,在一幢高CD=15m的甲楼顶端C处,测得乙楼底部B的俯角为63°,乙楼顶端A的仰角为25°.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数图象的顶点在原点O,经过点A(1,$\frac{1}{4}$);点F(0,1)在y轴上.直线y=-1与y轴交于点H.
二次函数图象的顶点在原点O,经过点A(1,$\frac{1}{4}$);点F(0,1)在y轴上.直线y=-1与y轴交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com