
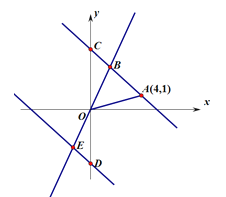
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象过点A(4,1)与正比例函数
的图象过点A(4,1)与正比例函数![]() (
(![]() )的图象相交于点B(
)的图象相交于点B(![]() ,3),与
,3),与![]() 轴相交于点C.
轴相交于点C.
(1)求一次函数和正比例函数的表达式;
(2)若点D是点C关于![]() 轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
(3)在坐标轴上是否存在一点![]() ,使
,使![]() .若存在请求出点
.若存在请求出点![]() 的坐标,若不存在请说明理由.
的坐标,若不存在请说明理由.
【答案】(1)一次函数表达式为:![]() ;正比例函数的表达式为:
;正比例函数的表达式为:![]() ;(2)E(-2,-3);(3)P点坐标为(
;(2)E(-2,-3);(3)P点坐标为(![]() ,0)或(
,0)或(![]() ,0)或(0,2)或(0,-2).
,0)或(0,2)或(0,-2).
【解析】
(1)将点A坐标代入![]() 可求出一次函数解析式,然后可求点B坐标,将点B坐标代入
可求出一次函数解析式,然后可求点B坐标,将点B坐标代入![]() 即可求出正比例函数的解析式;
即可求出正比例函数的解析式;
(2)首先求出点D坐标,根据DE∥AC设直线DE解析式为:![]() ,代入点D坐标即可求出直线DE解析式,联立直线DE解析式和正比例函数解析式即可求出点E的坐标;
,代入点D坐标即可求出直线DE解析式,联立直线DE解析式和正比例函数解析式即可求出点E的坐标;
(3)首先求出△ABO的面积,然后分点P在x轴和点P在y轴两种情况讨论,设出点P坐标,根据![]() 列出方程求解即可.
列出方程求解即可.
解:(1)将点A(4,1)代入![]() 得
得![]() ,
,
解得:b=5,
∴一次函数解析式为:![]() ,
,
当y=3时,即![]() ,
,
解得:![]() ,
,
∴B(2,3),
将B(2,3)代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
∴正比例函数的表达式为:![]() ;
;
(2)∵一次函数解析式为:![]() ,
,
∴C(0,5),
∴D(0,-5),
∵DE∥AC,
∴设直线DE解析式为:![]() ,
,
将点D代入得:![]() ,
,
∴直线DE解析式为:![]() ,
,
联立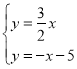 ,解得:
,解得:![]() ,
,
∴E(-2,-3);
(3)设直线![]() 与x轴交于点F,
与x轴交于点F,
令y=0,解得:x=5,
∴F(5,0),
∵A(4,1),B(2,3),
∴![]() ,
,
当点P在x轴上时,设P点坐标为(m,0),
由题意得:![]() ,
,
解得:![]() ,
,
∴P点坐标为(![]() ,0)或(
,0)或(![]() ,0);
,0);
当点P在y轴上时,设P点坐标为(0,n),
由题意得:![]() ,
,
解得:![]() ,
,
∴P点坐标为(0,2)或(0,-2),
综上所示:P点坐标为(![]() ,0)或(
,0)或(![]() ,0)或(0,2)或(0,-2).
,0)或(0,2)或(0,-2).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
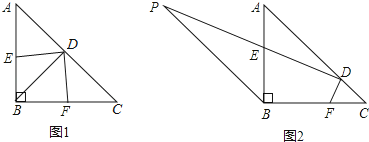
【题目】在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连结BD,E、F分别是AB、BC上的点,且DE⊥DF.、(1)如图1,若D为AC边上的中点.
(1)填空:∠C= ,∠DBC= ;
(2)求证:△BDE≌△CDF.
(3)如图2,D从点C出发,点E在PD上,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤1≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
(1)如图![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() ;
;
(2)如图![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,求证:
,求证:![]() .
.
(3)如图![]() ,
,![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
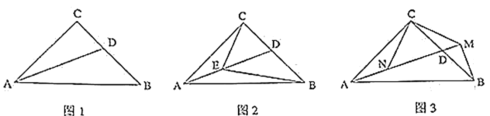
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.
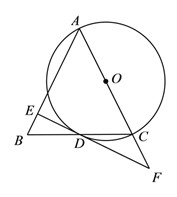
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形每组对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.请你在图①中补全特殊位置时的图形,并借助于所画图形探究问题的结论.
(问题解决)
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:
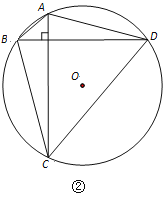
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=kx﹣10经过点A(12,0)和B(a,﹣5),双曲线y=![]() 经过点B.
经过点B.
(1)求直线y=kx﹣10和双曲线y=![]() 的函数表达式;
的函数表达式;
(2)点C从点A出发,沿过点A与y轴平行的直线向下运动,速度为每秒1个单位长度,点C的运动时间为t(0<t<12),连接BC,作BD⊥BC交x轴于点D,连接CD,
①当点C在双曲线上时,求t的值;
②在0<t<6范围内,∠BCD的大小如果发生变化,求tan∠BCD的变化范围;如果不发生变化,求tan∠BCD的值.
③当DC=![]() 时,请直接写出t的值.
时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某校要求没有读过四大名著的学生进行选读,将《西游记》、《三国演义》、《水浒传》《红楼梦》依次记为A、B、C、D,每本名著被选到的机会均等.
(1)学生小红计划选读两本名著,她恰好选读《西游记》和《水浒传》这两本名著的概率为多少?
(2)若学生小明和小刚各计划选读一本名著,他们两人恰好选读同一本名著的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com