
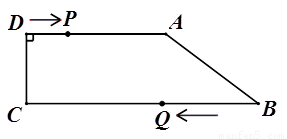
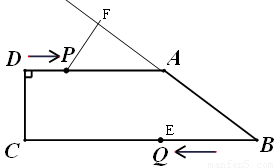
已知梯形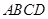 中,
中,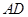 ∥
∥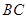 ,
,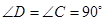 ,
,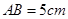 ,
,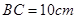 ,
,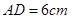 .动点
.动点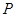 从
从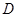 点开始以
点开始以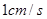 的速度沿线段
的速度沿线段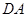 向
向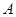 点运动,动点
点运动,动点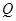 从点
从点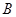 开始以
开始以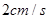 的速度沿线段
的速度沿线段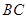 向
向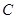 点运动.点
点运动.点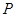 、点
、点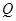 分别从
分别从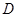 、
、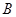 两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为
两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为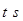 .
.
(1)求 的长;
的长;
(2)以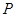 为圆心、
为圆心、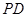 长为半径的
长为半径的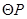 与直线
与直线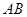 相切时,求
相切时,求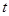 的值;
的值;
(3)是否存在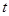 的值,使得以
的值,使得以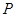 为圆心、
为圆心、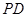 长为半径的
长为半径的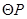 与以
与以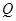 为圆心、
为圆心、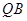 长为半径的
长为半径的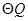 相切?若存在,求出
相切?若存在,求出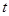 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)3cm;(2)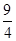 ;(3)
;(3)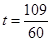 或
或
【解析】
试题分析:(1)作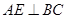 于
于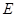 ,可得
,可得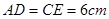 ,
,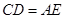 ,再根据勾股定理即可求得结果;
,再根据勾股定理即可求得结果;
(2)作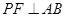 于
于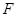 ,根据
,根据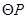 与直线
与直线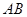 相切可得
相切可得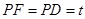 ,再结合
,再结合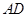 ∥
∥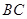 可证得△
可证得△ ∽△
∽△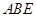 ,根据相似三角形的性质即可求得结果;
,根据相似三角形的性质即可求得结果;
(3)分两种情况:①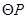 与
与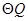 外切, ②
外切, ②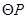 与
与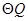 内切时,根据勾股定理依次分析即可求得结果.
内切时,根据勾股定理依次分析即可求得结果.
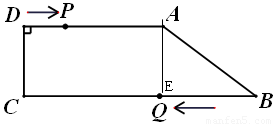
(1)作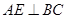 于
于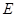 ,
,
则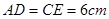 ,
,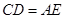
∵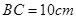
∴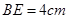
∴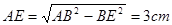
∴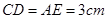 ;
;
(2)作 于
于
∵ 与直线
与直线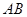 相切
相切
∴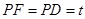
∵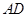 ∥
∥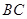
∴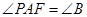
∴△ ∽△
∽△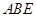 ,
,
∴ ,即
,即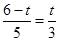 ,解得
,解得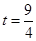 ;
;
(3)①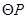 与
与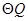 外切时,连
外切时,连 ,则
,则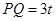 .作
.作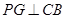 于
于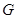 ,则
,则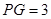 ,
,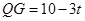
 ,解得
,解得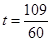
②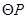 与
与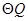 内切时,连
内切时,连 ,则
,则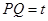 .作
.作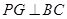 于
于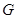 ,则
,则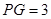 ,
,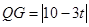 .
.
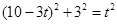 ,解得
,解得
经检验均符合题意.
综上: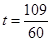 或
或 .
.
考点:动点综合题
点评:本题知识点较多,综合性强,难度较大,一般是中考压轴题,需要特别注意.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年上海市嘉定宝山九年级二模数学试卷(解析版) 题型:解答题
如图,已知梯形 中,
中,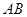 ∥
∥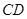 ,
, ,
,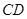 =4,点
=4,点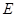 在边
在边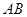 上,
上,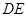 ∥
∥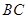 .
.

(1)若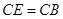 ,且
,且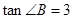 ,求
,求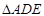 的面积;
的面积;
(2)若∠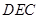 =∠
=∠ ,求边
,求边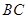 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com