
【题目】如图,A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是_____.
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是_____.

【答案】3
【解析】
先根据反比例函数图象上点的坐标特征及A,B两点的横坐标,求出A(2,2),B(4,1).再过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,根据反比例函数系数k的几何意义得出S△AOC=S△BOD=![]() ×4=2.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=
×4=2.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=![]() (BD+AC)CD=
(BD+AC)CD=![]() (1+2)×2=3,从而得出S△AOB=3.
(1+2)×2=3,从而得出S△AOB=3.
解:∵A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,
在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,
∴当x=2时,y=2,即A(2,2),
当x=4时,y=1,即B(4,1).
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,
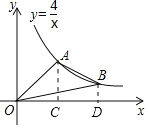
则S△AOC=S△BOD=![]() ×4=2.
×4=2.
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,
∴S△AOB=S梯形ABDC,
∵S梯形ABDC=![]() (BD+AC)CD=
(BD+AC)CD=![]() (1+2)×2=3,
(1+2)×2=3,
∴S△AOB=3.
故答案是:3.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
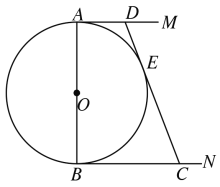
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.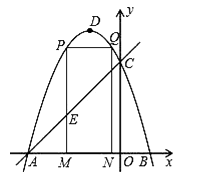
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= ![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
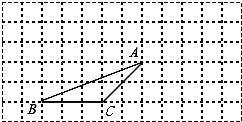
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
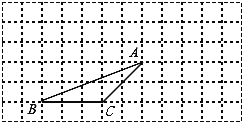
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将线段
,将线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,连接
,连接![]() ,
,![]() ,构成平行四边形
,构成平行四边形![]() .
.
(1)请写出点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上任意一个点(不与
上任意一个点(不与![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() ,试探索
,试探索![]() 、
、![]() 、
、![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com