Question

(1)已知关于x，y的方程组

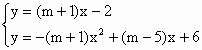
有两个实数解，求m的取值范围；

(2)在(1)的条件下，若抛物线y＝－(m＋1)x²＋(m－5)x＋6与x轴交于A、B两点，与y轴交于点C，且△ABC的面积等于12，确定此抛物线及直线y＝(m＋1)x－2的解析式；

(3)你能将(2)中所得的抛物线平移，使其顶点在(2)中所得的直线上吗？请写出一种平移方法．

Answer 1

答案：
解析：

解：(1)把方程①代入方程②，整理得(m＋l)x2＋6x－8＝0． 　　(i)当m≠－1时， 　　∵原方程组有两个实数解， 　　∴关于x的一元二次方程(m＋1)x2＋6x－8＝0必有两个不相等的实数根． 　　∴Δ＝36＋32(m＋1)＞0． 　　解得m＞－． 　　∴m＞－且m≠－1． 　　(ii)当m＝－1时，解得 　　 　　原方程组只有一个实数解． 　　∴m≠－1． 　　综上，m的取值范围是 　　m＞－且m≠－1． 　　(2)设点A(x1，0)、B(x2，0)，则x1、x2是关于x的一元二次方程(m＋1)x2－(m－5)x－6＝0的两个实数根． 　　∴x1＋x2＝，x1x2＝． 　　∵抛物线与y轴交于点C，∴C(0，6)． 　　∵S△ABC＝12，∴AB·6＝12． 　　∴|x2－x1|·9＝12． 　　∴|x2－x1|＝4． 　　∴(x1＋x2)2－4x1x2＝16． 　　∴()2＋＝16． 　　整理，得5m2＋6m－11＝0．解得 　　m1＝1，m2＝－． 　　经检验，m1＝1，m2＝－是此分式方程的解． 　　∵－＜－， 　　∴m2＝－不会题意，舍去． 　　又当m＝1时， 　　Δ＝[－(m－5)]2－4(m＋1)·(－6) 　　＝64＞0， 　　∴m＝1． 　　∴所求抛物线的解析式为 　　y＝－2x2－4x＋6； 　　所求直线解析式为 　　y＝2x－2． 　　(3)∵抛物线y＝－2x2－4x＋6的顶点坐标为(－1，8)，直线解析式为y＝2x－2(见答图)， 　　∴[方法一]将此抛物线向下平移12个单位，其顶点在直线y＝2x－2上． 　　[方法二]将此抛物线向右平移6个单位，其顶点在直线y＝2x－2上． 　　[方法三]……