
已知:抛物线![]() 与x轴交于点A(
与x轴交于点A(![]() ,0)、B(
,0)、B(![]() ,0)(A在B的左侧),与y轴交于点C.
,0)(A在B的左侧),与y轴交于点C.
(1)若m>1,△ABC的面积为6,求抛物线的解析式;
(2)点D在x轴下方,是(1)中的抛物线上的一个动点,且在该抛物线对称轴的左侧,作DE∥x轴与抛物线交于另一点E,作DF⊥x轴于F,作EG⊥x轴于点G,求矩形DEGF周长的最大值;
(3)若m<0,以AB为一边在x轴上方做菱形ABMN(∠NAB为锐角), P是AB边的中点,Q是对角线AM上一点,若![]() ,
,![]() ,当菱形ABMN的面积最大时,求点A的坐标.
,当菱形ABMN的面积最大时,求点A的坐标.
解:∵ 抛物线与x轴交于点A(x1,0)、B(x2,0),
∴ x1、x2是关于x的方程![]() 的解.
的解.
解方程,得![]() 或
或![]() .
.
(1)∵ A在B 的左侧,m>1,
∴![]() ,
,![]() .
.
 ∴ AB=m-1.
∴ AB=m-1.
抛物线与y轴交于C(0,m)点.
|
|
|
|
|
∴ 抛物线解析式为![]() .
.
(2)∵ 点D在(1)中的抛物线上,
∴ 设D(t, ![]() )(
)(![]() ).
).
∴ F(t,0),DF=![]() .
.
又抛物线对称轴是直线![]() ,DE与抛物线对称轴交点记为R(如图12),
,DE与抛物线对称轴交点记为R(如图12),
∴ DR=![]() ,DE=
,DE=![]() .
.
设矩形DEGF的周长为L,则 L=2(DF+DE).
∴ L =2(![]() +
+![]() )
)
=![]()
=![]() .
.
∵ ![]() ,
,
∴ 当且仅当![]() 时,L有最大值.
时,L有最大值.
当![]() 时,L最大=
时,L最大=![]() .
.
 ∴ 矩形周长的最大值为
∴ 矩形周长的最大值为![]() .
.
(3)∵ A在B 的左侧,m<0,
∴![]() ,
,![]() .
.
∴ AB=1-m.
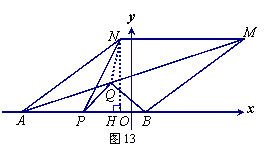
如图13,作NH⊥AB于H,连结QN.
在Rt△AHN中, ![]()
![]() .
.
设AH=4k(k>0), 则AN=5k,NH=3k.
∴ AP=![]() =
=![]() =
=![]() ,PH=AH -AP=
,PH=AH -AP=![]() =
=![]() ,PN=
,PN=![]() =
=![]() .
.
∵ 菱形ABMN是轴对称图形,
∴ QN=QB.
∴ PQ+QN = PQ+QB=6.
∵ PQ+QN≥PN(当且仅当P、Q、N三点共线时,等号成立).
∴ ![]()
![]() ,
,
解得 k≤![]() .
.
∵ S菱形ABMN=AB·NH=15 k2≤48.
∴ 当菱形面积取得最大值48时,k=![]() .
.
此时AB=5k=1-m =![]() .
.
解得 m=1-![]() .
.
∴ A点的坐标为(1-![]() ,0).
,0).


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,
抛物线y=ax2+bx+c的图象如图所示,已知该抛物线与x轴交于A、B两点,顶点为C,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.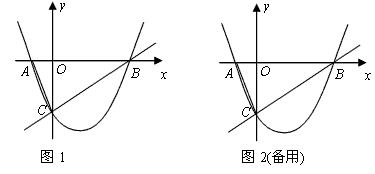
 的顶点坐标是
的顶点坐标是 ]
] 查看答案和解析>>
科目:初中数学 来源: 题型:
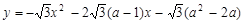 与x轴交于
与x轴交于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com