
【题目】如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的和距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,建立适当坐标系.
(1)求抛物线的解析式.
(2)求两盏景观灯之间的水平距离.

【答案】(1)y=﹣![]() (x﹣5)2+5(0≤x≤10);(2)5m.
(x﹣5)2+5(0≤x≤10);(2)5m.
【解析】整体分析:
(1)建立坐标系后,确定抛物线的顶点坐标,设解析式为y=a(x﹣5)2+5,把点(0,1)代入求a;(2)根据两盏景观灯的纵坐标是4,列方程求横坐标.
(1)根据题意建立坐标系,如图所示:

抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),
设抛物线的解析式是y=a(x﹣5)2+5,
把(0,1)代入y=a(x﹣5)2+5,
得a=﹣![]() ,
,
∴y=﹣![]() (x﹣5)2+5(0≤x≤10);
(x﹣5)2+5(0≤x≤10);
(2)由已知得两景观灯的纵坐标都是4,
∴4=﹣![]() (x﹣5)2+5,
(x﹣5)2+5,
∴![]() (x﹣5)2=1,
(x﹣5)2=1,
∴x1=![]() ,x2=
,x2=![]() .
.
∴![]() ﹣
﹣![]() =5.
=5.
所以两景观灯之间的水平距离为5米.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的![]() ;
;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
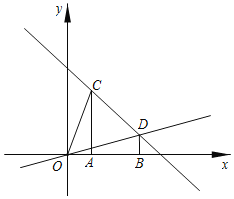
【题目】在平面直角坐标系中,过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .
.
(1)求直线![]() 和直线
和直线![]() 的解析式;
的解析式;
(2)点![]() 为直线
为直线![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,求此时点
为顶点的四边形为平行四边形?若存在,求此时点![]() 的横坐标;若不存在,请说明理由;
的横坐标;若不存在,请说明理由;
(3)若![]() 沿
沿![]() 方向平移(点
方向平移(点![]() 在线段
在线段![]() 上,且不与点
上,且不与点![]() 重合),在平移的过程中,设平移距离为
重合),在平移的过程中,设平移距离为![]() ,
,![]() 与
与![]() 重叠部分的面积记为
重叠部分的面积记为![]() ,试求
,试求![]() 与
与![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
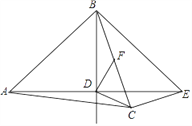
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5![]() -3
-3![]() +4
+4![]() -
-![]()
(2)(![]() -
-![]() -
-![]() )×(-36)
)×(-36)
(3)-![]() ―(1―0.5)÷
―(1―0.5)÷![]() ×[2+(-4)2]
×[2+(-4)2]
(4)(![]() -
-![]() )×52÷|-
)×52÷|-![]() |+(
|+(![]() )2019×42020
)2019×42020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 的长度是 ;
的长度是 ;
![]()
(2)若把(1)中点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,改为点
,改为点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,其他条件不变,请求出线段
,其他条件不变,请求出线段![]() 的长度(用含
的长度(用含![]() 、
、![]() 的式子表示);
的式子表示);
(3)若把(2)中点![]() 是线段
是线段![]() 上任意一点,改为点
上任意一点,改为点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
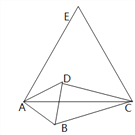
【题目】如图,四边形ABCD中,AD//BC,AD=AB=2,∠B=120°,∠ADC=150°,现以对角线AC为边向点D一侧作等边△ACE,则四边形ABCE的面积=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用如图所示矩形纸片的四个角都剪去一个边长为![]() 的正方形(阴影部分).并制成一个长方体纸盒。
的正方形(阴影部分).并制成一个长方体纸盒。
(1)用a,b,x表示纸片剩余部分的面积和纸盒的底面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com