
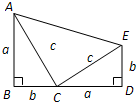
 伽菲尔德( Garfield,1881年任美国第20届总统)利用“三个直角三角形的面积和等于一个直角梯形的面积”(如图所示)证明了勾股定理,请你应用此图证明勾股定理.
伽菲尔德( Garfield,1881年任美国第20届总统)利用“三个直角三角形的面积和等于一个直角梯形的面积”(如图所示)证明了勾股定理,请你应用此图证明勾股定理.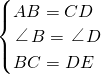 ,
,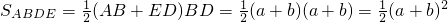 ,
,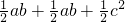 ,
,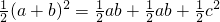 ,
,

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
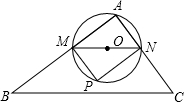 于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN,令AM=x.
于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN,令AM=x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
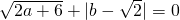 ,解关于x的不等式(a+2)x+b2>a-1.
,解关于x的不等式(a+2)x+b2>a-1.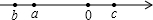
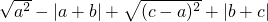 .
.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
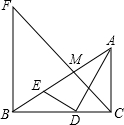 如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F
如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F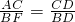 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com