
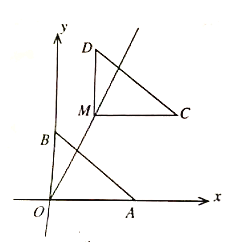
【题目】如图,点![]() 在直线
在直线![]() 上,点
上,点![]() 的坐标分别是
的坐标分别是![]() ,连接
,连接![]() ,将
,将![]() 沿射线
沿射线![]() 方向平移,使点O移动到点M,得到
方向平移,使点O移动到点M,得到![]() (点
(点![]() 分别对应点
分别对应点![]() ).
).
(1)填空:m的值为_____________,点C的坐标是______________;
(2)在射线![]() 上是否存在一点N,使
上是否存在一点N,使![]() ,如果存在,请求出点N的坐标;如果不存在,请说明理由;
,如果存在,请求出点N的坐标;如果不存在,请说明理由;
(3)连接![]() ,点P是射线
,点P是射线![]() 上一动点,请直接写出使
上一动点,请直接写出使![]() 是等腰三角形时点P的坐标.
是等腰三角形时点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) 或(0,0)或(
) 或(0,0)或(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() ).
).
【解析】
(1)当x=2时,y=2x=4,故:m=4,则点M的坐标为(2,4),由平移,可知:CM=AO=4,即可求解;
(2)存在,理由:分当NC在直线MC下方、上方,两种情况分别求解即可;
(3)分AD=AP、AD=PD、AP=PD三种情况,分别求解即可.
解:(1)当x=2时,y=2x=4,
∴m=4,∴点M的坐标为(2,4),
由平移,可知:CM=AO=4,
∴点C的坐标为(6,4),则点D(2,6).
故答案为:4;(6,4).
(2)存在,理由:
①当NC在直线MC下方时,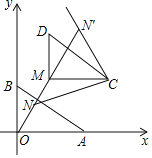
直线OM的表达式为:y=2x…①,
则tan∠MOB=![]() ,
,
∠NCM=∠BOM,则tan∠NCM=![]() ,
,
设直线NC的表达式为:y=![]()
将点C的坐标代入上式并解得:b=1,
则直线NC的表达式为:y=![]()
将①②联立并求解得:x=![]() ,
,
则点N(![]() ,
,![]() ) ;
) ;
②当NC在直线MC上方时,
同理可得:点N′(![]() ,
,![]() );
);
故点N(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() );
);
(3)设点P(x,2x),点D(2,6),点A(4,0),
则AD2=4+36=40,AP2=(x-4)2+4x2=5x2-8x+16,PD2=(x-2)2+(2x-6)2=5x2-28x+40,
①当AD=AP时,40=5x2-8x+16,解得:x=![]() ,
,
②当AD=PD时,同理可得:x=0或![]() ,
,
③当AP=PD时,同理可得:x=![]() ,
,
故点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) 或(0,0)或(
) 或(0,0)或(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
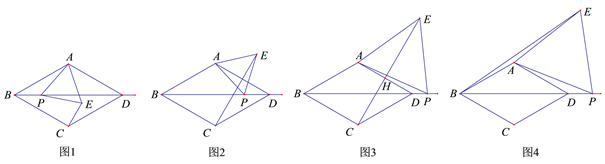
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
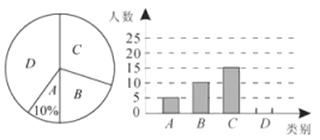
【题目】襄阳市文化底蕴深厚,旅游资源丰富,古隆中、习家池、鹿门寺三个景区是人们节假日游玩的热点景区.张老师对八(1)班学生“五·一”小长假随父母到这三个景区游玩的计划做了全面调查,凋奄分四个类别:A 游三个景区;B 游两个景区;C 游一个景区;D 不到这三个景区游玩.现根据调查结果绘制了不完整饷条形统计图和扇形统计图,请结合图中信息解答下列问题.
(1)八(1)班共有学生 人,在扇形统计图中,表示“B 类别”的扇形的圆心角的度数为 ;
(2)请将条形统计图补充完整:
(3)若张华、李刚两名同学,各自从三个景区中随机选一个作为5月1日游玩的景区,则他们同时选中古隆中的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
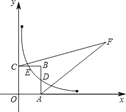
【题目】如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数![]() 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
(1)求反比例函数![]() 和直线OE的函数解析式;
和直线OE的函数解析式;
(2)求四边形OAFC的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
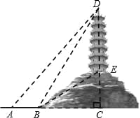
【题目】十堰市人民公园重阳塔也叫长寿塔,坐落在人民公园长寿山顶,八角形楼阁式塔.某人为了测量重阳塔的高度,他在山下与山脚![]() 在同一水平面的
在同一水平面的![]() 处测得塔尖点
处测得塔尖点![]() 的仰角为
的仰角为![]() ,再沿方向前进 45 米到达山脚点
,再沿方向前进 45 米到达山脚点![]() ,测得塔尖点
,测得塔尖点![]() 的仰角为
的仰角为![]() ,塔底点
,塔底点![]() 的仰角为
的仰角为![]() ,并画出了如图所示的示意图.请你根据相关数据求出塔
,并画出了如图所示的示意图.请你根据相关数据求出塔![]() 的高度.(
的高度.(![]() 结果保留整数)
结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程x2﹣kx+2=0中,k是投掷骰子所得的数字(1,2,3,4,5,6),则该二次方程有两个不等实数根的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
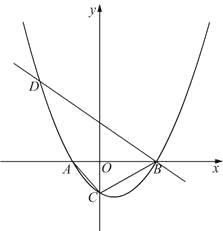
【题目】如图,已知抛物线![]() (
(![]() 为常数,且
为常数,且![]() )与
)与![]() 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与![]() 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线![]() 与抛物线的另一交点为D.
与抛物线的另一交点为D.
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)若在第一象限的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求![]() 的值;
的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止. 当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com