
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:阅读理解
| b |
| 2 |
| b |
| 2 |
 数形结合的思想方法
数形结合的思想方法查看答案和解析>>
科目:初中数学 来源: 题型:
 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.| 6 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
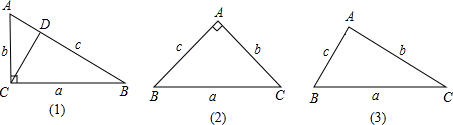
(1)观察下面两块三角尺,它们有一个共同的性质:∠A=2∠B,我们由此出发来进
行思考。

在图(1)中,作斜边AB上的高CD,由于∠B=30°,可知c=2b,于是AD=![]() ,
,
BD=c-![]() 。由于△CDB∽△ACB,可知
。由于△CDB∽△ACB,可知![]() =
=![]() ,即a2=c·BD。
,即a2=c·BD。
同理b2=c·AD。于是a2-b2=c(BD-AD)=c[(c-![]() )-
)-![]() ]=c(c-b)
]=c(c-b)
=c(2b-b)
=bc。对于图(2),由勾股定理有a2=b2+c2,由于b=c,故有a
这两块三角尺都具有性质a2-b2=bc。
在△ABC中,如果一个内角等于另一个内角的2倍,我们就称这种三角形为倍角三角
形。两块三角尺就都是特殊的倍角三角形。对于任意的倍角三角形,上面的性质仍然
成立吗?暂时把我们的设想作为一个猜测:
如图(3),在△ABC中,若∠CAB=2∠ABC,则a2-b2=bc。
在上述由三角尺的性质到猜想这一认识过程中,用到了下列四种数学思想方法中的哪
一种?选出一个正确的并将其序号填在括号内………………………………………( )
①分类的思想方法 ②转化的思想方法 ③由特殊到一般的思想方法 ④数形结合的
思想方法
(2)这个猜测是否正确?请证明。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,BD=c-
,BD=c- ,由于△CDB∽△ACB,可知,即a2=c•BD.同理b2=c•AD,于是a2-b2=c(BD-AD)=c(c-b)=bc.对于图(2),由勾股定理有a2=b2+c2,由于b=c,故也有a2-b2=bc.
,由于△CDB∽△ACB,可知,即a2=c•BD.同理b2=c•AD,于是a2-b2=c(BD-AD)=c(c-b)=bc.对于图(2),由勾股定理有a2=b2+c2,由于b=c,故也有a2-b2=bc. 数形结合的思想方法
数形结合的思想方法查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com