
【题目】如图,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,以线段
,以线段![]() 为边在第四象限内作等腰直角
为边在第四象限内作等腰直角![]() ,且
,且![]() .
.
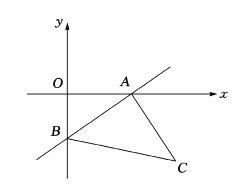
(1)试写出点![]() 的坐标:
的坐标: ![]() (_ _,_ ___),
(_ _,_ ___),![]() (_ ,_ )
(_ ,_ )
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的函数表达式
的函数表达式
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据坐标轴上的点的坐标特征,结合一次函数的解析式求出A、B两点的坐标;
(2)作CD⊥x轴于点D,由全等三角形的判定定理可得出△AOB≌△CDA,由全等三角形的性质可知AD=OB=3,CD=OA=4,故可得出C点坐标,
(3)使用待定系数法即可求出直线BC的解析式.
(1)(1)一次函数![]() 中,
中,
令y=0,解得x=4.
则点A的坐标是(4,0).
令x=0得y=-3.
则点B的坐标是(0,-3).
故答案为![]() ,
,![]() .
.
(2)过点C作CD⊥x轴,垂足为点D

∵![]() ,
,
∴![]() ,
,
又![]()
∴![]()
又![]() ,AB=AC
,AB=AC
∴△AOB≌△CDA
∴AD=OB=3,CD=OA=4
∴OD=7
∴C(7,﹣4)
(3)设直线BC的函数表达式为y=kx+b
把B(0,﹣3),C(7,﹣4)代入上式
得![]()
解之得
∴直线BC的函数表达式为y=![]() .
.


科目:初中数学 来源: 题型:
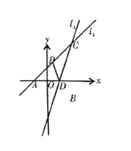
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)在![]() 轴上一点
轴上一点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)直线![]() 上一点
上一点![]() ,平面内一点
,平面内一点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,求点
全等,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
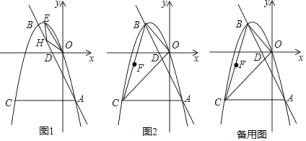
【题目】如图![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
![]() 求
求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
![]() 若点
若点![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() 点,连接
点,连接![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
![]() 如图
如图![]() ,连接
,连接![]() ,
,![]() 及
及![]() ,设点
,设点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上任意一点,将
上任意一点,将![]() 沿边
沿边![]() 翻折得到
翻折得到![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.一次函数y=![]() x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
x+1的图象L1交y轴于点A,一次函数y=﹣x+3的图象L2交x轴于点B,L1与L2交于点C.
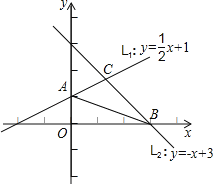
(1)求点A与点B的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ___________,当
___________,当![]() 时
时![]() ____________;
____________;
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;备用图
的图象;备用图
(3)结合画出的函数图象,解决问题:若关于![]() 的方程
的方程![]() 只有一个实数根,直接写出实数
只有一个实数根,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
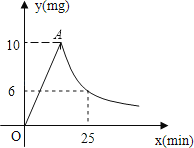
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-5,5),(-2,3).

(1)请在图中的网格平面内画出平面直角坐标系xOy;
(2)请画出△ABC关于y轴对称的△A1B1C1,并写出顶点A1,B1,C1的坐标
(3)请在x轴上求作一点P,使△PB1C的周长最小.请标出点P的位置(保留作图痕迹,不需说明作图方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知一次函数![]() 的图像与x轴交于点
的图像与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)在坐标系中能否找到点![]() ,使得
,使得![]() 且
且![]() ?如果能,求出满足条件的点
?如果能,求出满足条件的点![]() 的坐标;如果不能,请说明理由.
的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
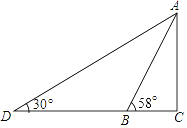
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com