Question

如图，圆B切y轴于原点O，过定点作圆B切线交圆于点P．已知

，抛物线经过A，P两点．

（1）求圆B的半径；

（2）若抛物线C经过点B，求其解析式；

（3）投抛物线C交y轴于点M，若三角形APM为直角三角形，求点M的坐标．

Answer 1

解：（1）连接BP，∵AP是圆B切线，∴AP⊥BP，

  

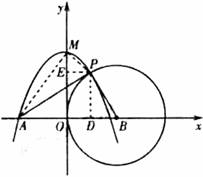
在直角三角形APB中，∵tan∠PAB=，

∴∠PAB=30°，∴sin∠PAB=

设圆B的半径为r，则sin∠PAB=

解得r=

(2)由（1）知AP=

过点P作PD⊥轴，交于点D，则AD==3，OD=，DP=3

∴点P的坐标为（，3）

又∵抛物线C经过A（-2，0）、B（2，0）、P（，3）三点，

∴设抛物线C解析式为

则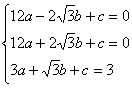，解得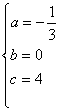

∴抛物线C解析式为

（3）过点P作PE⊥y轴，交于点E，连结PM、AM

设M（0,m）,则PM²=3+(m-3)²

又AM²=12+m²，则AP²=36

若∠AMP=90°，则AP²=AM²+PM²

∴36=3+(m－3)²+12+m²

即m²－3m－6=0,解得m=

 若∠APM=90°，则AM²=AP²+PM²

∴12+m²=36+3+(m-3)²,解得m=6

若∠PAM=90°，则PM²=AP²+AM²

∴3+(m－3)²=36+12+m²,解得m=－6

∴所求点M的坐标为（0，），（0，±6）