
(1)证明:连接DF,
∵CD是圆直径∴∠CFD=90°即DF⊥BC,
∵∠ACB=90°,∴DF∥AC,
∴∠BDF=∠A,
∵在⊙O中∠BDF=∠GEF,∴∠GEF=∠A.
(2)解:∵D是Rt△ABC斜边AB的中点,
∴DC=DA,
∴∠DCA=∠A,
又由(1)知∠GEF=∠A∴∠DCA=∠GEF,
又∵∠OME=∠EMC,
∴△OME∽△EMC相似,
∴
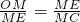
∴ME
2=OM×MC,
又∵ME=

∴OM×MC=
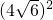
=96,
∵MD:CO=2:5,
∴OM:MD=3:2,∴OM:MC=3:8,
设OM=3xMC=8x,
∴3x×8x=96,
∴x=2,
直径CD=10x=20.
(3)解:∵Rt△ABC斜边AB的中线CD=20,
∴AB=40,
∵在Rt△ABC中,cos∠B=0.6=

,∴BC=24,
∴AC=32,
设直线AB的函数表达式为y=kx+b根据题意得A(32,0)B(0,24),
b=24,0×k+b=24解得
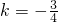
,32×k+b=0,
∴直线AB的函数解析式为y=-

x+24.
分析:(1)连接DF,根据CD是圆直径,可知∠CFD=90°即DF⊥BC,DF∥AC,推出∠BDF=∠A,在⊙O中∠BDF=∠GEF,所以∠GEF=∠A;
(2)根据D是Rt△ABC斜边AB的中点,DC=DA,∠DCA=∠A,可证明△OME与△EMC相似,所以,ME
2=OM×MC,结合MD:CO=2:5,OM:MD=3:2,OM:MC=3:8,设OM=3xMC=8x,可求x=2,则直径CD=10x=20;
(3)根据Rt△ABC斜边AB的中线CD=20可求得AB=40,cos∠B=0.6,BC=24,AC=32.设直线AB的函数表达式为y=kx+b把A(32,0)B(0,24)代入利用待定系数法求得,直线AB的函数解析式为y=-

x+24.
点评:主要考查了函数和几何图形的综合运用.
解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

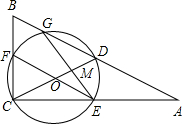 如图,在△ABC中∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G,F,E点.GE,CD的交点为M,且ME=4
如图,在△ABC中∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G,F,E点.GE,CD的交点为M,且ME=4 ,MD:CO=2:5.
,MD:CO=2:5. (1)证明:连接DF,
(1)证明:连接DF,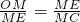 ∴ME2=OM×MC,
∴ME2=OM×MC, ∴OM×MC=
∴OM×MC=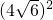 =96,
=96, ,∴BC=24,
,∴BC=24,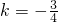 ,32×k+b=0,
,32×k+b=0, x+24.
x+24. x+24.
x+24.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为