
����Ŀ���ۺ�̽��
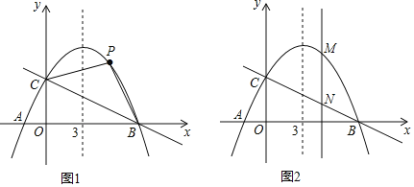
��֪������y��ax2+![]() x+4�ĶԳ�����ֱ��x��3����x���ཻ��A��B���㣨��B�ڵ�A�Ҳࣩ����y�ύ�ڵ�C��
x+4�ĶԳ�����ֱ��x��3����x���ཻ��A��B���㣨��B�ڵ�A�Ҳࣩ����y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��A��B��������ꣻ
��2����ͼ1������P����������B��C����֮���һ�����㣨����B��C�غϣ����Ƿ���ڵ�P��ʹ�ı���PBOC�������������ڣ����P�����꼰�ı���PBOC��������ֵ���������ڣ���˵�����ɣ�
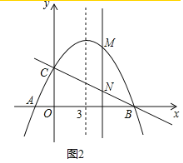
��3����ͼ2������M��������������һ�㣬����M��y���ƽ���ߣ���ֱ��BC�ڵ�N����MN��3ʱ��ֱ��д����M�����꣮
���𰸡���1�������ߵĽ���ʽΪ��y����![]() x2+
x2+![]() x+4����A������Ϊ(��2��0)����B������Ϊ(8��0)��2�����ڵ�P(4��6)��ʹ���ı���PBOC��������P������Ϊ(4��6)���ı���PBOC��������ֵΪ32��3����M������Ϊ(2��6)��(6��4)��(4��2
x+4����A������Ϊ(��2��0)����B������Ϊ(8��0)��2�����ڵ�P(4��6)��ʹ���ı���PBOC��������P������Ϊ(4��6)���ı���PBOC��������ֵΪ32��3����M������Ϊ(2��6)��(6��4)��(4��2![]() ��
��![]() ��1)��(4+2
��1)��(4+2![]() ����
����![]() ��1)
��1)
��������
��1�����������ߵĶԳ��᷽�̣����ɵõ�a��ֵ���Ӷ��õ���������ʽ���������A��B��ֵ��
��2�����ݴ���ϵ���������ֱ��BC�Ľ���ʽ�����P������Ϊ��x����![]() x2+
x2+![]() x+4��������P��PD��y�ᣬ��ֱ��BC�ڵ�D�����D������Ϊ(x����
x+4��������P��PD��y�ᣬ��ֱ��BC�ڵ�D�����D������Ϊ(x����![]() x+4)���������PD��ֵ������S�ı���PBOC��S��BOC+S��PBC���õ����κ�������ʽ�����ɵõ��𰸣�
x+4)���������PD��ֵ������S�ı���PBOC��S��BOC+S��PBC���õ����κ�������ʽ�����ɵõ��𰸣�
��3�����M������Ϊ(m����![]() m2+
m2+![]() m+4)�����N������Ϊ(m����
m+4)�����N������Ϊ(m����![]() m+4)����MN=|��
m+4)����MN=|��![]() m2+2m |������MN=3���г�����m�ķ��̣�������⣮
m2+2m |������MN=3���г�����m�ķ��̣�������⣮
��1���� �����ߵĶԳ����ǣ�ֱ��x��3��
�� ![]() ��3����ã�a����
��3����ã�a����![]() ��
��
�������ߵĽ���ʽΪ��y����![]() x2+
x2+![]() x+4��
x+4��
��y��0ʱ����![]() x2+
x2+![]() x+4��0�����x1����2��x2��8��
x+4��0�����x1����2��x2��8��
���A������Ϊ(��2��0)����B������Ϊ(8��0)��
��2����x��0ʱ��y����![]() x2+
x2+![]() x+4��4��
x+4��4��
���C������Ϊ(0��4)��
��ֱ��BC�Ľ���ʽΪ��y��kx+b��k��0����
��B(8��0)��C(0��4)����y��kx+b�ã�![]() ����ã�
����ã� ��
��
��ֱ��BC�Ľ���ʽΪ��y����![]() x+4��
x+4��
������ڵ�P��ʹ�ı���PBOC��������
���P��������x����![]() x2+
x2+![]() x+4������ͼ1��
x+4������ͼ1��
����P��PD��y�ᣬ��ֱ��BC�ڵ�D�����D������Ϊ(x����![]() x+4)��
x+4)��
��PD����![]() x2+
x2+![]() x+4��(��
x+4��(��![]() x+4)����
x+4)����![]() x2+2x��
x2+2x��
��S�ı���PBOC��S��BOC+S��PBC��![]() ��8��4+
��8��4+![]() PDOB
PDOB
��16+![]() ��8(��
��8(��![]() x2+2x)����x2+8x+16
x2+2x)����x2+8x+16
������x��4��2+32
����x��4ʱ���ı���PBOC�����������ֵ��32��
��0��x��8��
�����ڵ�P(4��6)��ʹ���ı���PBOC���������ı���PBOC��������ֵΪ32��
��3�����M������Ϊ(m����![]() m2+
m2+![]() m+4)�����N������Ϊ(m����
m+4)�����N������Ϊ(m����![]() m+4)����ͼ2��
m+4)����ͼ2��
��MN��|��![]() m2+
m2+![]() m+4��(��
m+4��(��![]() m+4)|��|��
m+4)|��|��![]() m2+2m |��
m2+2m |��
�֡� MN��3��
�� |��![]() m2+2m |��3��
m2+2m |��3��
��0��m��8ʱ����![]() m2+2m��3��0����ã�m1��2��m2��6��
m2+2m��3��0����ã�m1��2��m2��6��
����M������Ϊ(2��6)��(6��4)��
��m��0��m��8ʱ����![]() m2+2m +3��0����ã�m3��4��2
m2+2m +3��0����ã�m3��4��2![]() ��m4��4+2
��m4��4+2![]() ��
��
����M������Ϊ(4��2![]() ��
��![]() ��1)��(4+2
��1)��(4+2![]() ����
����![]() ��1)��
��1)��
�𣺵�M������Ϊ(2��6����(6��4����(4��2![]() ��
��![]() ��1����(4+2
��1����(4+2![]() ����
����![]() ��1����
��1����




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��һ��ֱ��������ֽƬ������
��һ��ֱ��������ֽƬ������![]() ��
��![]() ��С�������Ƶ�
��С�������Ƶ�![]() ��ʱ����ת��
��ʱ����ת��![]() �õ�
�õ�![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() .
.

��1����ͼ1����![]() ʱ��
ʱ��![]() ����ֱ�����߶�
����ֱ�����߶�![]() ��������λ�ù�ϵ����˵������.
��������λ�ù�ϵ����˵������.
��2����ͼ2����![]() ����
����![]() Ϊ����������ʱ�Ķ���.
Ϊ����������ʱ�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() Ϊ
Ϊ![]() �����Բ��
�����Բ��![]() ������
������![]() ��������
��������![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() .
.
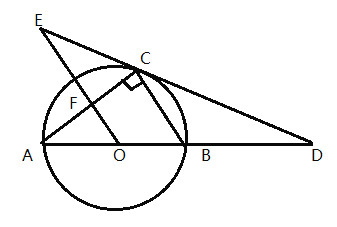
��1���ж�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2����![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
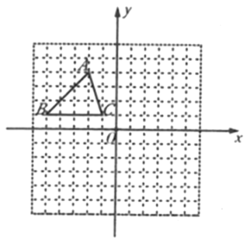
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ��![]() �����������ֱ���
�����������ֱ���![]() .��
.��![]() ��ԭ��
��ԭ��![]() ˳ʱ����ת90���õ�
˳ʱ����ת90���õ�![]() ������ƽ��ֱ������ϵ������
������ƽ��ֱ������ϵ������![]() ����д��
����д��![]() �Ķ�������.
�Ķ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��
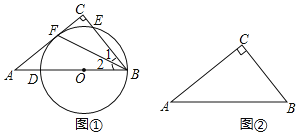
��1����ͼ�٣���![]() ��б��
��б��![]() �ϣ��Ե�
�ϣ��Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶��Բ��
��Ϊ�뾶��Բ��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() �����
�����![]() �����ڵ�
�����ڵ�![]() ����֤��
����֤��![]() ��
��
��2����ͼ������![]() ��ʹ����������������
��ʹ����������������
��Բ���ڱ�![]() �ϣ��ھ�����
�ϣ��ھ�����![]() �������
�������![]() ����
����
���߹���ͼ��ֻ������ͼ�ۼ�����Ҫ��д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �Ľ�������ʽΪ
�Ľ�������ʽΪ![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ������
������![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
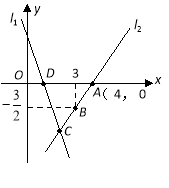
��1�����![]() �����ꣻ
�����ꣻ
��2����ֱ��![]() �Ľ�������ʽ��
�Ľ�������ʽ��
��3����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
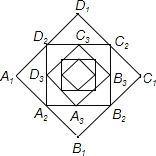
����Ŀ����ͼ��С�������˱߳�Ϊ2�ĵ�һ��������A1B1C1D1����������������Ȼ��ֱ�ȡ������A1B1C1D1�ıߵ��е�A2��B2��C2��D2�����˵ڶ���������A2B2C2D2������������������ͬ���ķ����������˵�����������A3B3C3D3�������������������ɴ˿ɵã�������������A6B6C6D6������ǣ�������
A.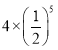 B.
B.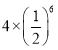 C.
C.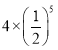 D.
D.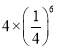
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧѡ��һ������־Ը�ߣ������ԡ����ԣ����С����С�����е�һ����ί�����ͨ��ץ����ȷ����ѡ���������£��ڲ����IJ�����װ�г���ɫ֮�����ͬ��2�������1������С����ȡ��һ����ס��ɫ��Żأ�Ȼ��С����ȡ��һ����������ȡ�������Ǻ�����С��ʤ����������ȡ��������һ��һ�̣���С��ʤ��������Ϊ��������˫����ƽ�������б�������״ͼ�ķ������з�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�DE��BC��EF��AB��
��1����֤����ADE�ס�EFC��
��2�����AB=6��AD=4����![]() ��ֵ.
��ֵ.
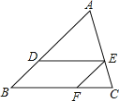
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com