
【题目】如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)见解析;(2) 图中阴影部分的面积为![]() .
.
【解析】
(1)连接OF,AO,根据题意可得∠ABF=∠AFB=∠EBF=30°,再利用OB=OF,证明AB∥OF,即可解答
(2)先利用等弧对等角求出△AOF是等边三角形,再证明S△ABF=S△AOF,即可解答
(1)证明:连接OF,AO,
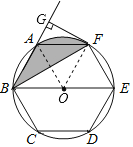
∵AB=AF=EF,
∴![]() ,
,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵![]() ,
,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2![]() ,
,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的一带一路经济发展战略,树立品牌意识,我市质检部分别对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图:
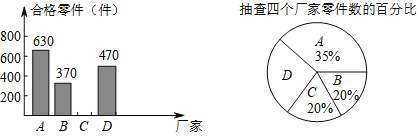
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 度;
(2)抽查C厂家的合格率零件为 件,并将图1补充完整;
(3)通过计算说明A、C两厂家谁的合格率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .点
.点![]() 是
是![]() 的中点,在
的中点,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
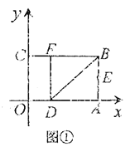
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
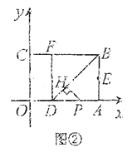
(Ⅱ)如图②,若点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 于
于![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() ,试用关于
,试用关于![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅲ)在![]() 轴、
轴、![]() 轴上分别存在点
轴上分别存在点![]() 、
、![]() ,使得四边形
,使得四边形![]() 的周长最小,请直接写出四边形
的周长最小,请直接写出四边形![]() 的周长最小值.
的周长最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
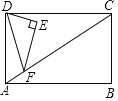
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
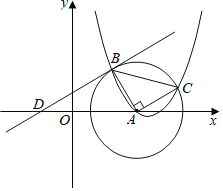
【题目】如图,已知![]() 的圆心为点
的圆心为点![]() ,抛物线
,抛物线![]() 过点
过点![]() ,与
,与![]() 交于
交于![]() 两点,连接
两点,连接![]() 、
、![]() ,且
,且![]() ,
,![]() 两点的纵坐标分别是2、1.
两点的纵坐标分别是2、1.
(1)请直接写出点![]() 的坐标,并求
的坐标,并求![]() 的值;
的值;
(2)直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() (与点
(与点![]() 不重合)在该直线上,且
不重合)在该直线上,且![]() ,请判断点
,请判断点![]() 是否在此抛物线上,并说明理由;
是否在此抛物线上,并说明理由;
(3)如果直线![]() 与
与![]() 相切,请直接写出满足此条件的直线解析式.
相切,请直接写出满足此条件的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体育达标情况,随机抽取![]() 名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
测试成绩(分) |
|
|
|
|
|
人数(人) |
|
|
|
|
|
(1)该校九年级有![]() 名学生,估计体育测试成绩为
名学生,估计体育测试成绩为![]() 分的学生人数;
分的学生人数;
(2)该校体育老师要对本次抽测成绩为![]() 分的甲、乙、丙、丁
分的甲、乙、丙、丁![]() 名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com