
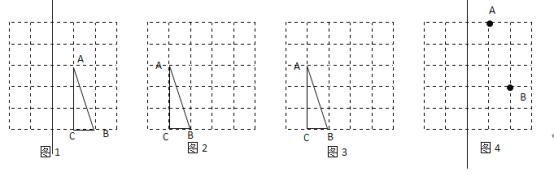
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
【答案】(1)图见解析;(2)图见解析;(3)图见解析;(4)图见解析
【解析】
(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 即可;
即可;
(2)如解图2,连接CH,交AB于点D,利用SAS证出△ACB≌△CGH,从而得出∠BAC=∠HCG,然后利用等量代换即可求出∠CDB=90°;
(3)如解图3,连接CP交AB于点E,利用矩形的性质可得AE=BE;
(4)如解图4,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM,根据平行四边形的性质和两点之间线段最短即可推出此时MN即为所求.
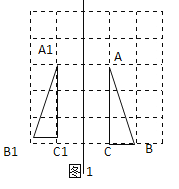
解:(1)分别找到A、B、C关于直线l的对称点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,如图1所示,
,如图1所示,![]() 即为所求;
即为所求;
(2)如图2所示连接CH,交AB于点D,
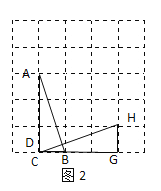
在△ACB和△CGH中
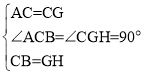
∴△ACB≌△CGH
∴∠BAC=∠HCG
∵∠BAC+∠ABC=90°
∴∠HCG+∠ABC=90°
∴∠CDB=90°
∴CD为△ABC的高,故CD即为所求;
(3)如图3所示,连接CP交AB于点E
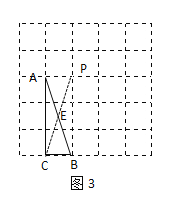
由图可知:四边形ACBP为矩形
∴AE=EB
∴CE为△ABC的中线,故CE即为所求;
(4)如图4所示,找出点A关于l的对称点A1,设点A1正下方的格点为C,连接CB,交直线l于点N,设点B正上方的格点为D,连接A1D,交直线l于点M,连接AM
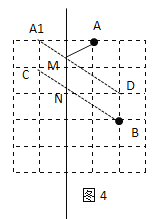
根据对称性可知:AM=A1M
由图可知:A1C=BD=1个单位长度,A1C∥BD∥直线l
∴四边形A1CBD为平行四边形
∴A1D∥BC
∴四边形A1CNM和四边形MNBD均为平行四边形
∴A1M=CN,MN=BD=1个单位长度
∴AM=CN
∴AM+NB=CN+NB=CB,
根据两点之间线段最短,此时AM+NB最小,而MN=1个单位长度为固定值,
∴此时![]() 最小,故此时MN即为所求.
最小,故此时MN即为所求.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上运动(不与点
上运动(不与点![]() 重合).
重合).
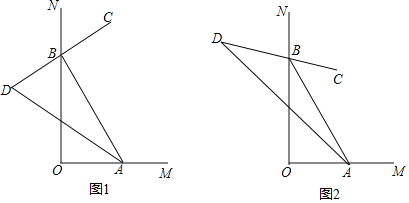
(1)如图1,![]() 是
是![]() 的平分线,
的平分线,![]() 的反方向延长线与
的反方向延长线与![]() 的平分线交于点
的平分线交于点![]() .
.
①若![]() ,则
,则![]() 为多少度?请说明理由.
为多少度?请说明理由.
②猜想:![]() 的度数是否随
的度数是否随![]() 、
、![]() 的移动发生变化?请说明理由.
的移动发生变化?请说明理由.
(2)如图2,若![]() ,
,![]() ,则
,则![]() 的大小为 度(直接写出结果);
的大小为 度(直接写出结果);
(3)若将“![]() ”改为“
”改为“![]() (
(![]() )”,且
)”,且![]() ,
,![]() ,其余条件不变,则
,其余条件不变,则![]() 的大小为 度(用含
的大小为 度(用含![]() 、
、![]() 的代数式直接表示出米).
的代数式直接表示出米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
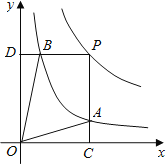
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
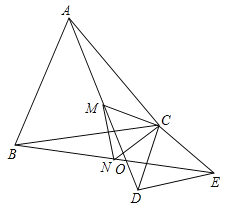
【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下4个结论:①
的中点.以下4个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() 以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
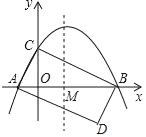
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2)
(1)求抛物线的表达式;
(2)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线的对称轴上是否存在点P,使△BMP与△ABD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.
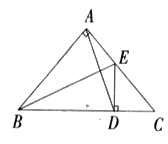
(1)请你写出图中所有的等腰三角形;
(2)请你判断AD与BE垂直吗?并说明理由.
(3)如果BC=10,求AB+AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com