
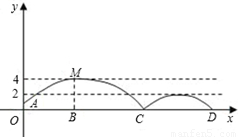
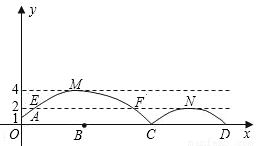
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取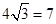 )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取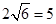 )
)
(1) ;(2)13;(3)10.
;(2)13;(3)10.
【解析】
试题分析:(1)依题意应用待定系数法可得抛物线的表达式;(2)令y=0可求出x的两个值,再按实际情况筛选;(3)本题有多种解法.如图可得第二次足球弹出后的距离为CD,相当于将抛物线AEMFC向下平移了2个单位可得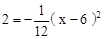 解得x的值即可知道CD、BD.
解得x的值即可知道CD、BD.
试题解析:如图,设第一次落地时,抛物线的表达式为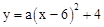 .
.
由已知:当x=0时y=1,∴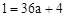 ,解得
,解得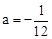 .
.
∴足球开始飞出到第一次落地时,该抛物线的表达式为 .
.
(2)令y=0,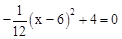 ,解得
,解得 (舍去).
(舍去).
∴足球第一次落地距守门员约13米.
(3)如图,第二次足球弹出后的距离为CD,
根据题意:CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),
∴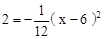 ,解得
,解得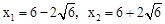 .
.
∴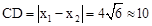 (米).
(米).
考点:1.二次函数的应用;2. 待定系数法的应用;3.曲线上点的坐标与方程的关系.


科目:初中数学 来源: 题型:
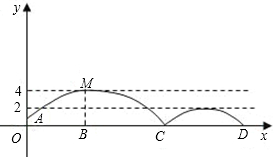 弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 6 |
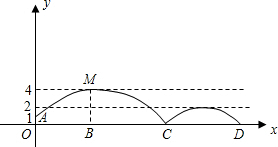
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出(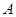 在
在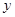 轴上),运动员乙在距
轴上),运动员乙在距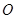 点6米的
点6米的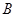 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点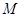 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.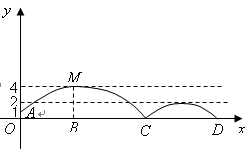
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点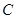 距守门员多少米?(取
距守门员多少米?(取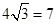 )
)
(3)运动员乙要抢到第二个落点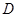 ,他应再向前跑多少米?
,他应再向前跑多少米?
(取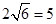 )
)
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(吉林长春卷)数学(解析版) 题型:解答题
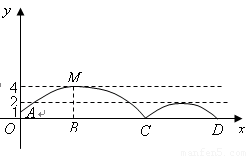
如图,足球场上守门员在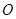 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的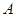 处飞出(
处飞出(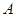 在
在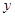 轴上),运动员乙在距
轴上),运动员乙在距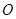 点6米的
点6米的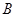 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点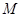 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点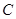 距守门员多少米?(取
距守门员多少米?(取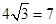 )
)
(3)运动员乙要抢到第二个落点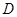 ,他应再向前跑多少米?
,他应再向前跑多少米?
(取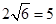 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com