
已知:m、n是方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图像经过点A(
的图像经过点A(![]() )、B(
)、B(![]() ).
).
(1) 求这个抛物线的解析式;
(2) 设(1)中抛物线与![]() 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线![]() 的顶点坐标为
的顶点坐标为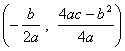
(3) P是线段OC上的一点,过点P作PH⊥![]() 轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
轴,与抛物线交于H点,若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.

解(1)解方程![]() 得
得![]()
由![]() ,有
,有![]()
所以点A、B的坐标分别为A(1,0),B(0,5).
将A(1,0),B(0,5)的坐标分别代入![]() .
.
得![]() 解这个方程组,得
解这个方程组,得![]()
所以,抛物线的解析式为![]()
(2)由![]() ,令y=0,得
,令y=0,得![]()
解这个方程,得![]()
所以C点的坐标为(-5,0).由顶点坐标公式计算,得点D(-2,9).
过D作x轴的垂线交x轴于M.
则![]()
![]() ,
,
![]()
所以,![]() .
.
(3)设P点的坐标为(a,o)
因为线段BC过B、C两点,所以BC所在的值线方程为y=x+5.
那么,PH与直线BC的交点坐标为E(a,a+5),
PH与抛物线![]() 的交点坐标为H(a,-a2-4a+5).
的交点坐标为H(a,-a2-4a+5).
由题意,得①![]() ,即
,即![]()
解这个方程,得![]() 或
或![]() (舍去)
(舍去)
②![]() ,即
,即![]()
解这个方程,得![]() 或
或![]()
![]() (舍去)
(舍去)
P点的坐标为![]() 或
或![]() .
.


科目:初中数学 来源:天津模拟题 题型:解答题
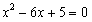 的两个实数根,且m<n,抛物线
的两个实数根,且m<n,抛物线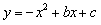 的图像经过点A(m,0)、B(0,n)。
的图像经过点A(m,0)、B(0,n)。 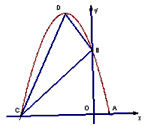
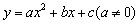 的顶点坐标为
的顶点坐标为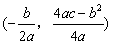 )
)查看答案和解析>>
科目:初中数学 来源:模拟题 题型:解答题
已知:t1、t2是方程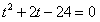 的两个实数根,且t1<t2,抛物线
的两个实数根,且t1<t2,抛物线 的图象经过点
的图象经过点
A(t1,0),B(0,t2)。

 的面积S与x之间的函数关系式,并写出自变量的取值范围;
的面积S与x之间的函数关系式,并写出自变量的取值范围;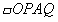 的面积为24时,是否存在这样的点P,使
的面积为24时,是否存在这样的点P,使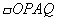 为正方形?若存在,求出P点坐标;若不存在,说明理由。
为正方形?若存在,求出P点坐标;若不存在,说明理由。查看答案和解析>>
科目:初中数学 来源: 题型:
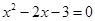 的两根,且sin∠OBC=
的两根,且sin∠OBC=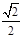 .
.
查看答案和解析>>
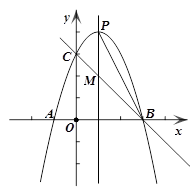
科目:初中数学 来源:2011-2012学年四川乐山市区中考模拟数学试卷(解析版) 题型:解答题
如图,抛物线y=ax2+bx+c与x轴交于A(x1,0)、B(x2,0)两点,与y轴交于C点,对称轴与抛物线相交于点P,与直线BC相交于点M,连接PB.已知x1、x2
恰是方程 的两根,且sin∠OBC=
的两根,且sin∠OBC= .
.

1.求该抛物线的解析式;
2.抛物线上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;若不存在,说明理由
3.在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相等,若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com