【题目】如图，
面积为
，第一次操作：分别延长
至点
使
，顺次连结，得到
，第二次操作：分别延长
至点
，使
，顺次连结，得到
， ．．按此规律，要使得到的三角形的面积超过
，至少经过_________次操作．
【答案】4
【解析】
先根据已知条件求出△A1B1C1及△A2B2C2的面积，再根据两三角形的倍数关系求解即可．
解：△ABC与△A1BB1底相等（AB=A1B），高为1：2（BB1=2BC），故面积比为1：2，
∵△ABC面积为1，
∴△A1B1B的面积=2．
同理可得，△C1B1C的面积=2，△AA1C的面积=2，
∴△A1B1C1的面积=△C1B1C的面积+△AA1C的面积+△A1B1B的面积+△ABC的面积=2+2+2+1=7；
同理可证：△A2B2C2的面积=7△A1B1C1的面积=49，
第三次操作后的面积为7×49=343，
第四次操作后的面积为7×343=2401．
故按此规律，要使得到的三角形的面积超过2016，最少经过4次操作．
故答案为：4．
科目：初中数学 来源： 题型：
【题目】如图，长方形
中，
，
，点
是
的中点，动点
从
点出发，以每秒
的速度沿
运动，最终到达点.若点运动的时间为
秒，那么当
_____________秒时，
的面积等于
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据阅读内容，在括号内填写推理依据．
如果两条平行线被三条直线所截，那么一对内错角的角平分线一定互相平行．
已知：AB∥CD，EM平分∠AEF，FN平分∠EFD
求证： EM∥FN
证明：
∵AB∥CD
∴∠AEF=∠DFE （ ）
∵EM平分∠AEF
∴∠MEF=
∠ AEF （ ）
∵FN平分∠EFD
∴∠EFN=∠ EFD （ ）
∴∠MEF=∠ EFN
∴ EM ∥FN （ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰三角形
的底边
长为
，面积是
， 腰
的垂直平分线
分别交
边于
点．若点
为边的中点，点
为线段EF上一动点，则
周长的最小值为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，给出四个结论：
①c＞0；
②若点B（﹣ 
，y1）、C（﹣ 
，y2）为函数图象上的两点，则y1＜y2；
③2a﹣b=0；
④ 
＜0，
其中，正确结论的个数是（ ）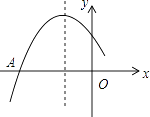
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】郴州市一座美丽的旅游城市，吸引了很多的外地游客，某旅行社对5月份本社接待的外地游客来郴州旅游的首选景点作了一次抽样调查．调查结果如下图表：(如图)
景点 | 频数 | 频率 |
东江湖 |
|
|
莽山 |
|
|
飞天山 |
| |
苏仙岭 |
|
|
万华岩 |
|
|
此次共调查了多少人?
请将以上图表补充完整．
该旅行社预计6月份接待外地来郴的游客
人，请你估计首选去东江湖的人数约有多少人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方形ABCD在平面直角坐标系中，AD∥BC∥x轴，AB∥DC∥y轴，x轴与y轴夹角为90°，点M，N分别在xy轴上，点A（1，8），B（1，6），C（7，6），D（7，8）．
（1）连接线段OB、OD、BD，求△OBD的面积；
（2）若长方形ABCD在第一象限内以每秒0.5个单位长度的速度向下平移，经过多少秒时，△OBD的面积与长方形ABCD的面积相等请直接写出答案；
（3）见备用图，连接 OB，OD，OD交BC于点E，∠BON的平分线和∠BEO的平分线交于点F．
①当∠BEO的度数为n，∠BON的度数为m时，求∠OFE的度数．
②请直接写出∠OFE和∠BOE之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有个填写运算符号的游戏：在“ 1□3□9□7” 中的每个□内，填入
，
，
，
中的某一个（可重复使用），然后计算结果．
（1）计算：
；
（2）若13×9□7= -4，请推算□内的符号；
（3）在“1□3□9-7”的□内填入符号后，使计算所得数最小，直接写出这个最小数是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
