
【题目】如图,在![]() 中,
中,![]() . 将线段
. 将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,
,![]() 是边
是边![]() 上的一动点,连接
上的一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
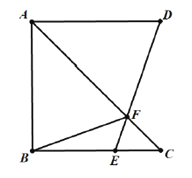
(2)点![]() 在边
在边![]() 上,且
上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
①判断![]() 与
与![]() 的位置关系,并证明你的结论;②连接
的位置关系,并证明你的结论;②连接![]() ,若
,若![]() ,请直接写出线段
,请直接写出线段![]() 长度的最小值.
长度的最小值.
【答案】(1)见解析;(2)①![]() ,见解析;②
,见解析;②![]() ,见解析.
,见解析.
【解析】
(1)根据旋转的性质易得:AB=AD,∠BAF=∠DAF,结合AF=AF可证![]() 即可得出结论;
即可得出结论;
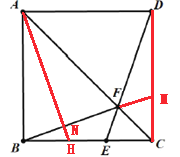
(2)①在![]() 上取
上取![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,易证四边形
,易证四边形![]() 是正方形;通过证明
是正方形;通过证明![]() 得
得![]() ,由
,由![]() 知
知![]() ,易证
,易证![]() .再证明
.再证明![]() 即可;
即可;
②根据当点![]() 运动过程中,
运动过程中,![]() 始终成立,点
始终成立,点![]() 的轨迹在以
的轨迹在以![]() 为直径的圆上求解即可.
为直径的圆上求解即可.
(1)证明:∵![]()
∴![]()
∵![]()
∴![]()
在![]() 和
和![]() 中,
中,
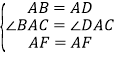 ,
,
∴![]() (
(![]() )
)
∴![]() ;
;
(2)①证明:在![]() 上取
上取![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]()
由(1)得∠DAC=∠DCA,AD=AB=BC,
∵![]() ,
,
∴四边形![]() 是平行四边形
是平行四边形
∵![]()
∴四边形![]() 是正方形
是正方形
∵ BH=CE,AB=DC,![]()
∴![]() (
(![]() )
)
∴![]()
∵![]() (
(![]() )
)
∴![]()
∴![]()
即![]()
∵在![]() 中,
中,![]()
∴![]()
∴![]()
即![]()
②![]()
理由:由第二问可知,当点![]() 运动过程中,
运动过程中, ![]() 始终成立,点
始终成立,点![]() 的轨迹在以
的轨迹在以![]() 为直径的圆上,
为直径的圆上,![]() 与圆的交点即为最小值
与圆的交点即为最小值![]() .
.


科目:初中数学 来源: 题型:
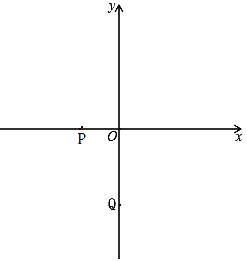
【题目】如图,已知:P(-1,0),Q(0,-2).
(1)求直线PQ的函数解析式;
(2)如果M(0,![]() )是线段OQ上一动点,抛物线
)是线段OQ上一动点,抛物线![]() 经过点M和点P,
经过点M和点P,
①求抛物线![]() 与
与![]() 轴另一交点N的坐标(用含
轴另一交点N的坐标(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
②若PN=![]() 是,抛物线
是,抛物线![]() 有最大值
有最大值![]() +1,求此时
+1,求此时![]() 的值;
的值;
③若抛物线![]() 与直线PQ始终都有两个公共点,求
与直线PQ始终都有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是40元,根据市场调查:在一段时间内,销售单价是50元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>50),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润ω元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) | ① |
销售玩具获得利润ω(元) | ② |
(2)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于54元,且商场要完成不少于400件的销售任务,求商场销售该品牌玩具获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)当![]() 时,利用根的判别式判断方程根的情况,
时,利用根的判别式判断方程根的情况,
(2)若方程有两个相等的非零实数根,写出一组满足条件的![]() 的值,并求此时方程的根.
的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
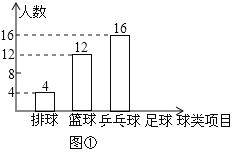

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与x轴、y轴交于点
分别与x轴、y轴交于点![]() 和点B,直线
和点B,直线![]() 分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为
分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为![]() 的中点。
的中点。
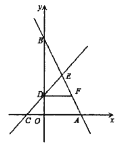
(1)求直线![]() 的解析式;
的解析式;
(2)过点D作![]() 轴,交直线
轴,交直线![]() 于点F,求
于点F,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
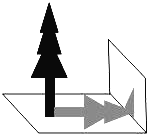
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.5m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1m,又测得地面的影长为1.5m,请你帮她算一下,树高为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
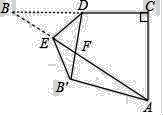
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com