
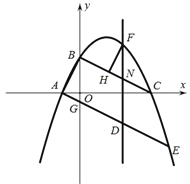
【题目】如图所示,在平面直角坐标系中,抛物线![]() 与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点
与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点![]() 为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
(1)求抛物线的表达式及直线BC的表达式;
(2)在点D运动的过程中,当FN的值最大时,在线段BC上是否存在一点H,使得FNH与ABC相似,如果存在,求出此时H点的坐标;
(3)当DF=4时,连接DC,四边形ABCD先向上平移一定单位长度后,使点D落在x轴上,然后沿x轴向左平移n(1n4)个单位长度,用含n的表达式表示平移后的四边形与原四边形重叠部分的面积S(直接写出结果).

【答案】(1)直线![]() 的解析式为
的解析式为![]() ,抛物线的解析式为
,抛物线的解析式为![]() ;(2)存在,点
;(2)存在,点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]()
![]() .
.
【解析】
(1)将点A(-1,0),C(4,0)代入![]() 得出方程组,再解方程组求出a,b即可;根据B、C两点坐标利用待定系数法求出直线BC的解析式即可;
得出方程组,再解方程组求出a,b即可;根据B、C两点坐标利用待定系数法求出直线BC的解析式即可;
(2)如图2中,设![]() ,则
,则![]() ,构建二次函数求出FN最大时,点F的坐标,证明
,构建二次函数求出FN最大时,点F的坐标,证明![]() 是直角三角形,观察图象可知,只有
是直角三角形,观察图象可知,只有![]() 时,
时,![]() ,求出直线FH的解析式,利用方程组即可求出点H的坐标;
,求出直线FH的解析式,利用方程组即可求出点H的坐标;
(3)根据![]() ,列出方程,求出m的值,分两种情形分别求解即可.
,列出方程,求出m的值,分两种情形分别求解即可.
解:(1)把![]() ,
,![]() 代入
代入![]()
得到![]() ,
,
解得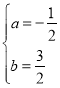 ,
,
∴抛物线的解析式为![]() ,
,
∵![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则有![]() ,
,
解得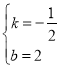 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
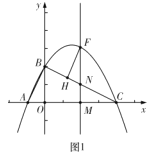
(2)如图1中,设![]() ,则
,则![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() 时,
时,![]() 的值最大,此时
的值最大,此时![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 相似,
相似,
观察图象可知,只有![]() 时,
时, ![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由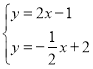 ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(3)∵![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() 或3.
或3.
①当![]() 时,如图2中,
时,如图2中,![]() 时,重叠部分是四边形
时,重叠部分是四边形![]() ,
,
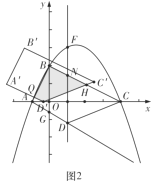
![]() ;
;
如图3中,![]() 时,重叠部分是
时,重叠部分是![]() ,
,
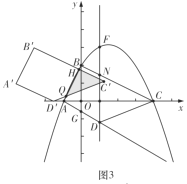
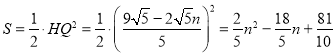 .
.
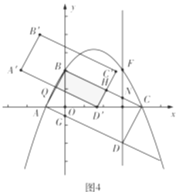
②当![]() 时,如图4中,
时,如图4中,![]() 时,重叠部分是矩形
时,重叠部分是矩形![]() .
.
![]()
![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
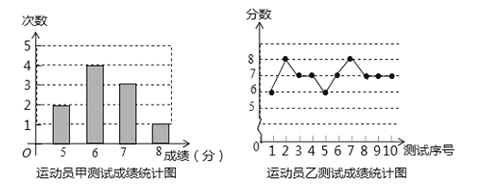
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
运动员丙测试成绩的平均数和众数都是7,
(1)成绩表中的![]() __________,
__________,![]() _________;
_________;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从乙手中传出,球传一次甲得到球的概率是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州中学在“读书日”期间购进一批图书, 需要用大小两种规格的纸箱来装运.![]() 个大纸箱和
个大纸箱和![]() 个小纸箱一次可以装
个小纸箱一次可以装![]() ,本书
,本书![]() 个大纸箱和
个大纸箱和![]() 个小纸箱--次可以装
个小纸箱--次可以装![]() 本书.
本书.
(1)一个大纸箱和一个小纸箱分别可以装多少本书?
(2)如果一共购入![]() 本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
本书,每个纸箱恰好装满,分别需要用多少个大、小纸箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销量较好的肉馅粽(咸)、豆沙馅粽(甜)、红枣馅粽(甜)、蛋黄馅粽(咸)(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
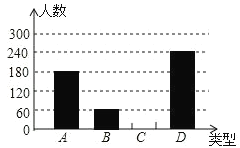
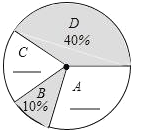
请根据以上信息回答:
(1)本次参加抽样调查的市民有多少人?
(2)将两幅不完整的图补充完整;
(3)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 与x轴,y轴分别交于点A,B,点
与x轴,y轴分别交于点A,B,点![]() 在第一象限内,连结
在第一象限内,连结![]() ,
,![]() ,
,![]() .动点P在
.动点P在![]() 上从点A向终点B匀速运动,同时,动点Q在
上从点A向终点B匀速运动,同时,动点Q在![]() 上从点C向终点O匀速运动,它们同时到达终点,连结
上从点C向终点O匀速运动,它们同时到达终点,连结![]() 交
交![]() 于点D.
于点D.
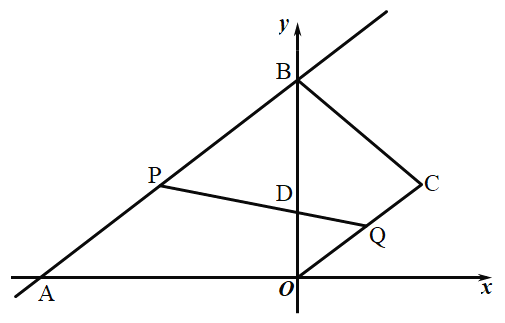
(1)求点B的坐标和a的值;
(2)当点Q运动到![]() 中点时,连结
中点时,连结![]() ,求
,求![]() 的面积;
的面积;
(3)作![]() 交直线
交直线![]() 于点R.
于点R.
①当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长度;
的长度;
②记![]() 交
交![]() 于点E,连结
于点E,连结![]() ,则
,则![]() 的最小值为__________.(直接写出答案)
的最小值为__________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),B(﹣1,0),与y轴交于点C,连接AC,点P是直线AC上方的抛物线上一动点(异于点A,C),过点P作PE⊥x轴,垂足为E,PE与AC相交于点D,连接AP.
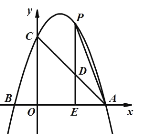
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)①求直线AC的解析式;
②是否存在点P,使得△PAD的面积等于△DAE的面积,若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,且
,且![]() 的面积为2.
的面积为2.
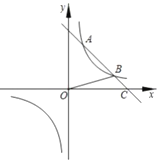
(1)求反比例函数的表达式;
(2)将直线![]() 向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线
向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线![]() 向下平移了几个单位长度?
向下平移了几个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意;B级:满意;C级:基本满意;D级:不满意),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
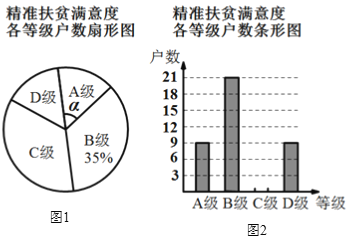
(1)本次抽样调查测试的建档立卡贫困户的总户数______.
(2)图1中,∠α的度数是______,并把图2条形统计图补充完整.
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的人数约为多少户?
(4)调查人员想从5户建档立卡贫困户(分别记为![]() )中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户
)中随机选取两户,调查他们对精准扶贫政策落实的满意度,请用列表或画树状图的方法求出选中贫困户![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com