
【题目】如图,平面直角坐标系中有4个点:A(0,2),B(﹣2,﹣2),C(﹣2,2),D(3,3).
(1)在正方形网格中画出△ABC的外接圆⊙M,圆心M的坐标是 ;
(2)若EF是⊙M的一条长为4的弦,点G为弦EF的中点,求DG的最大值;
(3)点P在直线MB上,若⊙M上存在一点Q,使得P、Q两点间距离小于1,直接写出点P横坐标的取值范围.

【答案】(1)(-1,0);(2)6;(3)﹣![]() <x<
<x<![]() 或﹣2﹣
或﹣2﹣![]() <x<﹣2+
<x<﹣2+![]() ;
;
【解析】
(1)画出△ABC的外接圆即可解决问题;
(2)当点G在线段DM延长线上时DG最大,此时DG=DM+GM,
(3)分两种情形构建方程即可即可解决问题;
(1)如图所示;M(-1,0);
故答案为(-1,0).
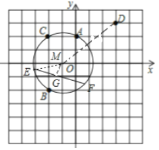
(2)连接MD,MG,ME,
∵点G为弦EF的中点,EM=FM=![]() ,
,
∴MG⊥EF,
∵EF=4,
∴EG=FG=2,
∴MG=![]() =1,
=1,
∴点G在以M为圆心,1为半径的圆上,
∴当点G在线段DM延长线上时DG最大,此时DG=DM+GM,
∵DM=![]() =5,
=5,
∴DG的最大值为5+1=6;
(3)设P点的横坐标为x,
当P点位于线段MB及延长线上且P、Q两点间距离等于1,时,![]() ,
,
∴![]() 或
或![]()
解得|xp|=2+![]() 或2-
或2-![]() ,
,
∵此时P点在第三象限,
∴x<0,
∴x=-2-![]() 或-2+
或-2+![]() ,
,
即当P、Q两点间距离小于1时点P横坐标的取值范围为-2-![]() <x<-2+
<x<-2+![]() ;
;
当P点位于线段BM及延长线上且P、Q两点间距离等于1时,则PQ:AM=|x|:|xM|,
![]() ,
,
解得|x|=![]() ,
,
∵此时P点在第一或二象限,
∴x=±![]() ,
,
即当P、Q两点间距离小于1时点P横坐标的取值范围为-![]() <x
<x![]() ;
;
综上所述,点P横坐标的取值范围为-![]() <x
<x![]() 或-2-
或-2-![]() <x<-2+
<x<-2+![]() .
.


科目:初中数学 来源: 题型:
【题目】观察下列![]() 个命题:其中真命题是( ).
个命题:其中真命题是( ).
(![]() )直线
)直线![]() 、
、![]() 、
、![]() ,如果
,如果![]() 、
、![]() ,那么
,那么![]() .
.
(![]() )三角形的三个内角中至少有两个锐角.
)三角形的三个内角中至少有两个锐角.
(![]() )平移变换中,各组对应点连成的两线段平行(或共线)且相等.
)平移变换中,各组对应点连成的两线段平行(或共线)且相等.
(![]() )三角形的外角和是
)三角形的外角和是![]() .
.
A.(![]() )(
)(![]() )B.(
)B.(![]() )(
)(![]() )C.(
)C.(![]() )(
)(![]() )D.(
)D.(![]() )(
)(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
(1)求抛物线的解析式;
(2)设点M(1,m),当MB+MD的值最小时,求m的值;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;
(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC延长线于点F.

(1)求证:四边形ABCD是菱形;
(2)若∠ABC=45°,BC=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读可以增进人们的知识也能陶治人们的情操。我们要多阅读,多阅读有营养的书。因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,整理后的数据如下表(表中信息不完整)。图1和图2是根据整理后的数据绘制的两幅不完整的统计图.
阅读时间分组统计表 | ||
组别 | 阅读时间x(h) | 人数 |
A |
| a |
B |
| 100 |
C |
| b |
D |
| 140 |
E |
| c |
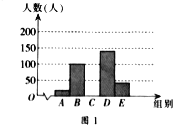
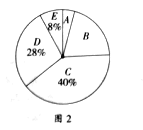
请结合以上信息解答下列问题
(1)求a,b,c的值;
(2)补全图1所对应的统计图;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点(3,2)。
的图象经过点(3,2)。
(1)求这个二次函数的关系式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当x>0时,求使y≥2的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()

A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
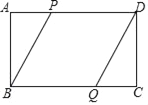
【题目】如图,矩形ABCD中,点P是线段AD上任意一点,点Q为BC上一点,且AP=CQ.
(1)求证:BP=DQ;
(2)若AB=4,且当PD=5时四边形PBQD为菱形.求AD为多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com