
【题目】请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴围成的
轴围成的![]() 的面积为
的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 坐标并判断
坐标并判断![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的面积为
的面积为![]() ,求
,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数与![]() 轴的交点关于
轴的交点关于![]() 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与![]() 轴的交点为“对心点”.
轴的交点为“对心点”.

(1)写出一个![]() 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;
(2)直线![]() 经过点
经过点![]() 和
和![]() ,直线
,直线![]() 的“对心函数”直线
的“对心函数”直线![]() 与
与![]() 轴的交点
轴的交点![]() 位于点
位于点![]() 的上方,且直线
的上方,且直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 为直线
为直线![]() 的“对心点”.点
的“对心点”.点![]() 是动直线
是动直线![]() 上不与
上不与![]() 重合的一个动点,且
重合的一个动点,且![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图,直线![]() 与其“对心函数”直线
与其“对心函数”直线![]() 的交点
的交点![]() 位于第一象限,
位于第一象限,![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的“对心点”,点
的“对心点”,点![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ;一动点
;一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() ,再沿线段
,再沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() 后停止,点
后停止,点![]() 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为![]() 秒,求直线
秒,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场调查表明:某种一周内水果的销售率y(销售率= ![]() )与价格倍数x(价格倍数=
)与价格倍数x(价格倍数= ![]() )的关系满足函数关系y=﹣
)的关系满足函数关系y=﹣ ![]() x+
x+ ![]() (1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
(1≤x≤5.5).根据有关规定,该商品售价不得超过进货价格的2倍,同时,一周内未售出的水果直接废弃.某商场希望通过销售该种水果可获取的最大利润率是( )
A.120%
B.80%
C.60%
D.40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2018年举行迎新春首届灯展,承办方计划在现场安装小彩灯和大彩灯,已知:安装5个小彩灯和4个大彩灯共需155元;安装7个小彩灯和6个大彩灯共需225元.
(1)安装1个小彩灯和1个大彩灯各需多少元.
(2)若承办方安装小彩灯和大彩灯的数量共300个,费用不超过5000元,则最多安装大彩灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
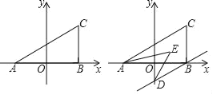
【题目】如图,在平面坐标系中,A(a,0),B(b,0),C(x,y)且满足(a+b)2+|a﹣b﹣4|=0,y=![]() +2.
+2.
(1)求三角形ABC的面积;
(2)若过B作BD∥AC交y轴于D,且AE、DE平分∠CAB、∠ODB,如图,求∠AED的度数;
(3)在y轴上是否存在点P,①使得△ABC和△ACP的面积相等,若存在,求出P点的坐标:若不存在,请说明理由;②若△ACP的面积是△ABC面积的2018倍成立,直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com