
【题目】如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=![]() 的图象上,求过点A的反比例函数的解析式.
的图象上,求过点A的反比例函数的解析式.
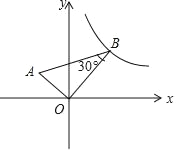
【答案】反比例函数的解析式为y=﹣![]() .
.
【解析】试题分析:
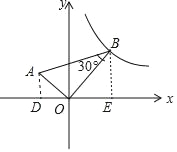
如图,作AD⊥x轴于D,BE⊥x轴于E,由点B在![]() 的图象上,可设其坐标为B(m,
的图象上,可设其坐标为B(m, ![]() ),则OE=m,BE=
),则OE=m,BE=![]() ,在Rt△AOB中,由∠B=30°可得OB=
,在Rt△AOB中,由∠B=30°可得OB=![]() OA,再证△AOD∽△OBE,即可由相似三角形的性质把OD、AD用含“m”的代数式表达出来,从而可表达出点A的坐标,这样即可求得过点A的反比例函数的解析式了.
OA,再证△AOD∽△OBE,即可由相似三角形的性质把OD、AD用含“m”的代数式表达出来,从而可表达出点A的坐标,这样即可求得过点A的反比例函数的解析式了.
试题解析:
作AD⊥x轴于D,BE⊥x轴于E,如图,设B(m, ![]() )
)
在Rt△ABO中,∵∠B=30°,
∴OB=![]() OA,
OA,
∵∠AOD=∠OBE,
∴Rt△AOD∽Rt△OBE,
∴![]() ,即
,即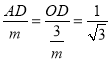 ,
,
∴AD= ![]() ,OD=
,OD=![]() ,
,
∴A点坐标为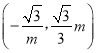 ,
,
设点A所在反比例函数的解析式为![]() ,
,
∴k=![]() ,
,
∴点B所在反比例函数的解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】《庄子·天下》:“一尺之棰,日取其半,万世不竭.”意思是说:一尺长的木棍,每天截掉一半,永远也截不完.我国智慧的古代人在两千多年前就有了数学极限思想,今天我们运用此数学思想研究下列问题.
(规律探索)
(1)如图1所示的是边长为1的正方形,将它剪掉一半,则S阴影1=1-![]() =__________;
=__________;
如图2,在图1的基础上,将阴影部分再裁剪掉—半,则S阴影2=1-![]() -(
-(![]() )2=_______;
)2=_______;
同种操作,如图3,S阴影3=1-![]() -(
-(![]() )2-(
)2-(![]() )3=__________;
)3=__________;
如图4,S阴影4=1-![]() -(
-(![]() )2-(
)2-(![]() )3-(
)3-(![]() )4=___________;
)4=___________;
……
若同种地操作n次,则S阴影n=1-![]() -(
-(![]() )2-(
)2-(![]() )3-…-(
)3-…-(![]() )n=_________.
)n=_________.
(规律归纳)
(2)直接写出![]() +
+![]() +
+![]() +…+
+…+![]() 的化简结果:_________.
的化简结果:_________.
(规律应用)
(3)直接写出算式![]() +
+![]() +
+![]() +…+
+…+![]() 的值:__________.
的值:__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县盛产不知火和脐橙两种水果 ,某公司计划用两种型号的汽车运输不知火和脐橙到外地销售,运输中要求每辆汽车都要满载满运,且只能装运一种水果.若用3辆汽车装运不知火,2辆汽车装运脐橙可共装载33吨,若用2辆汽车装运不知火,3辆汽车装运脐橙可共装载32吨.
(1)求每辆汽车可装载不知火或脐橙各多少吨?
(2)据调查,全部销售完后,每吨不知火可获利700元,每吨脐橙可获利500元,计划用20辆汽车运输,且脐橙不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为28的平行四边形纸片ABCD中,AB=7,∠BAD=45°,按下列步骤进行裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
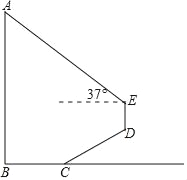
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 厘米/秒的速度移动;点
厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 厘米/秒的速度移动,如果
厘米/秒的速度移动,如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间,那么:
(秒)表示移动的时间,那么:

(1)如图1,当![]() 为何值时,线段
为何值时,线段![]() 的长度等于线段
的长度等于线段![]() 的长度?
的长度?
(2)如图2,当![]() 为何值时,
为何值时,![]() 与
与![]() 的长度之和是长方形
的长度之和是长方形![]() 周长的
周长的![]() ?
?
(3)如图3,点![]() 到达点
到达点![]() 后继续以相同速度沿
后继续以相同速度沿![]() 边运动,到达点
边运动,到达点![]() 后停止运动;点
后停止运动;点![]() 到达点
到达点![]() 后继续以相同速度沿
后继续以相同速度沿![]() 边运动,当点
边运动,当点![]() 停止运动时点
停止运动时点![]() 也停止运动.当点
也停止运动.当点![]() 在
在![]() 边上运动时,
边上运动时,![]() 为何值可使线段
为何值可使线段![]() 的长度等于线段
的长度等于线段![]() 长度的一半?
长度的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆摩托车同时从相距20km的A,B两地出发,相向而行.图中l 1,l 2分别表示甲、乙两辆摩托车到A地的距离s(km)与行驶时间t(h)的函数关系.则下列说法错误的是( )

A.乙摩托车的速度较快B.经过0.3小时甲摩托车行驶到A,B两地的中点
C.当乙摩托车到达A地时,甲摩托车距离A地![]() kmD.经过
kmD.经过![]() 小时两摩托车相遇
小时两摩托车相遇
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:我们可以将任意三位数记为![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分别表示该数的百位数字,十位数字和个位数字,且
分别表示该数的百位数字,十位数字和个位数字,且![]() ).显然
).显然![]() .
.
材料二:若一个三位数的百位数字,十位数字和个位数字均不为![]() ,则称之为“生数”,比如
,则称之为“生数”,比如![]() 就是一个“生数”,将“生数”的三个数位上的数字交换顺序,可产生出
就是一个“生数”,将“生数”的三个数位上的数字交换顺序,可产生出![]() 个新的“生数”,比如由
个新的“生数”,比如由![]() 可以产生出
可以产生出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这
这![]() 个新“生数”,将这
个新“生数”,将这![]() 个数相加,得到的和
个数相加,得到的和![]() 称为由“生数”
称为由“生数”![]() 生成的“完全数”
生成的“完全数”
问题:(1)求证:任意一个“完全数”都可以整除![]() ;
;
(2)若一个四位正整数![]() (
(![]() ,
,![]() 是整数)是由一个“生数”
是整数)是由一个“生数”![]() (
(![]() ,
,![]() ,
, ![]() 、
、![]() 是整数)产生的“完全数”,请求出这个“生数”
是整数)产生的“完全数”,请求出这个“生数”![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com