Question

已知关于2x²+kx-1=0．
（1）求证：该方程一定有两个不相等的实数根．
（2）若已知该方程的一个根是-1，请求出另一个根．

Answer 1

【答案】分析：（1）利用根的判别式△=b²-4ac进行判断即可；
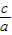
（2）利用根与系数的关系x₁•x₂=-进行计算即可．
解答：（1）证明：∵△=k²-4×2×（-1）=k²+4＞0，
∴该方程一定有两个不相等的实数根；

（2）解：设另一个根为x₁，根据根与系数的关系可得：x₁•x₂=-，
∵一个根是-1，
∴x₁•（-1）=-，
解得：x₁=．
点评：此题主要考查了根的判别式以及根与系数的关系，关键是掌握一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．