
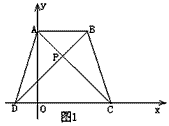
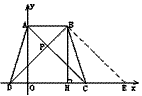
(1)若BC=10,A(0,8),求点D的坐标;
(2)若BC=13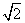 ,AB+CD=34,求过点B的反比例函数的解析式;
,AB+CD=34,求过点B的反比例函数的解析式;
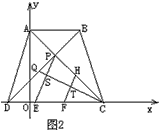
(3)如图2,在PD上有一点Q,连结CQ,过P作PE⊥CQ交CQ于S,交DC于E,在DC上取EF=DE,过F作
FH⊥CQ交CQ于T,交PC于H,当Q在PD上运动时,(不与P、D重合),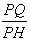 的值是否发生变化?若变化,求出变化范围;若不变,求出其值。
的值是否发生变化?若变化,求出变化范围;若不变,求出其值。
解:(1)在等腰梯形ABCD中,AD=BC=10,
又 点A的坐标为(0,8)
∴ OA=8,
∴ OD=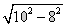 =6,
=6,
∴点D的坐标为(-6,0)。
(2)作BH⊥DE于H,过B点作BE∥AC交x轴于点E ,
∵ AB∥CE, BE∥AC,
∴ ABEC是平行四边形,
∴ AB=CE,BE=AC,
又 AC=BD,
∴ BE=BD,
而AC⊥BD, AB∥CE,
∴ ∠DPC=∠DBE=90° ,
∵ BH⊥DE
∴BH=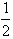 DE=
DE=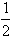 (DC+CE)=
(DC+CE)=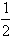 (DC+AB)=
(DC+AB)=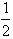 ×34=17,
×34=17,
∵BC=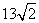 ,
,
∴CH=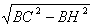 =7,
=7,
∴ OH=AB=CE=HE-HC=17-7=10,
∴点B的坐标为(10,17),
∴ 过B点的反比例函数的解析式为: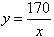 。
。 
(3)过点D作DN∥PC交PE的延长线于点M,交HF的延长线于点N,过点M作MI∥EF交BN于点I ,易证四边形EFIM和四边形MNHP是平行四边形,
∴MI=EF=DE,MN=PH,
又∵∠EDM=∠IMN,∠DEM=∠EFI=∠MIN,
∴△EDM≌△IMN
∴DM=MN,
∵∠PDM=∠CPQ=90°,∠DPM=∠QCP=90°-∠SPC
由(2)知:∠BDC=45°,而∠DPC=90°,
∴PD=PC,
∴△PDM≌△CPQ,
∴DM=PQ=PH,
∴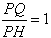


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
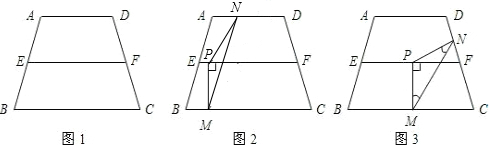
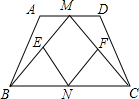 (2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:
(2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com