
【题目】某天快递配送员张强一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,这天他从出发点开始所走的路程(单位:![]() )记录如下:
)记录如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)这天送完最后一个快递时,张强在出发点的什么方向?距离出发点有多远?
(2)如果张强送完快递时,需立刻返回出发点,那么他这天送快递(含返回)共耗油多少升(每千米耗油![]() )?
)?
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
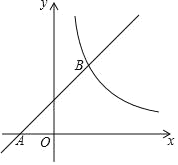
【题目】如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=![]() (x>0)的图象交于B(a,4).
(x>0)的图象交于B(a,4).
(1)求一次函数和反比例函数的表达式;
(2)设M(m﹣2,m)是直线AB上一点,过M作MN∥x轴,交反比例函数y=![]() (x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
(x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从家步行到公交车站台,等公交车去学校. 图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 他等公交车时间为6min
C. 他步行的速度是100m/min D. 公交车的速度是350m/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产![]() 两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产![]() 种购物袋
种购物袋![]() 个,每天共获利
个,每天共获利![]() 元.
元.
成本(元/个) | 售价(元/个) | |
| 2 | 2.3 |
| 3 | 3.5 |
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
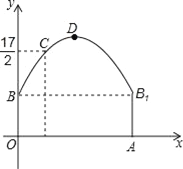
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若代数式(4x2-mx-3y+4)-(8nx2-x+2y-3)的值与字母x的取值无关,求代数式(-m2+2mn-n2)-2(mn-3m2)+3(2n2-mn)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com