
【题目】定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”. 例如:等腰直角三角形就是“半角三角形”.在钝角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 边于点
边于点![]() .点
.点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(1)若![]() ,点
,点![]() 在
在![]() 延长线上.
延长线上.
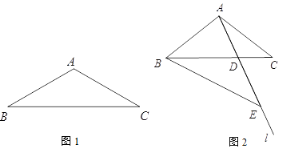
① 当![]() ,点
,点![]() 恰好为
恰好为![]() 中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
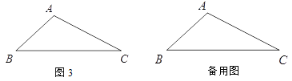
② 如图2,若![]() ,图中是否存在“半角三角形”(△
,图中是否存在“半角三角形”(△![]() 除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
(2)如图3,若![]() ,保持
,保持![]() 的度数与(1)中②的结论相同,请直接写出
的度数与(1)中②的结论相同,请直接写出![]() ,
,![]() ,
,![]() 满足的数量关系:______.
满足的数量关系:______.
【答案】(1)① 如图,见解析;△![]() 或△
或△![]() 或△
或△![]() 或△
或△![]() ; ②存在,“半角三角形”为△
; ②存在,“半角三角形”为△![]() ;证明见解析;(2)
;证明见解析;(2)![]() 或
或![]() .
.
【解析】
(1)①根据题干描述作出图形即可,利用等腰三角形的性质,根据“一个内角是另外一个内角的一半”的三角形符合题意,可得出结果.②延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() ,构造全等三角形△
,构造全等三角形△![]() ≌△
≌△![]() .再利用全等三角形的性质以及相关角度的转化,可求得
.再利用全等三角形的性质以及相关角度的转化,可求得![]() ,从而可得出结果.
,从而可得出结果.
(2)由(1)中②可知,![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接BF,构造全等三角形△
,连接BF,构造全等三角形△![]() ≌△
≌△![]() ,进而可得出
,进而可得出![]() .因为
.因为![]() ,所以以
,所以以![]() 为圆心,
为圆心,![]() 长为半径作圆与直线
长为半径作圆与直线![]() 一定有两个交点,当第一种情况成立时,必定存在一个与它互补的
一定有两个交点,当第一种情况成立时,必定存在一个与它互补的![]() ,所以可得出另外一种情况.
,所以可得出另外一种情况.
(1)① 如图,

图中的一个 “半角三角形”:△![]() 或△
或△![]() 或△
或△![]() 或△
或△![]() ;
;
② 存在,“半角三角形”为△![]() .
.
延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.

∵![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在△![]() 和△
和△![]() 中,
中,

∴ △![]() ≌△
≌△![]() .
.
∴ ![]() ,
,![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴![]() .
.
∴∠BAE=2∠BEA,
∴△![]() 为“半角三角形”.
为“半角三角形”.
(2)![]() 或
或![]() .
.
解:①延长![]() 到点
到点![]() ,使得
,使得![]() ,连接BF,
,连接BF,

∵![]() ,
,![]() ,
,
∴△![]() ≌△
≌△![]() .
.
过点![]() 分别作
分别作![]() 于点
于点![]() ,
,
![]() 于点
于点![]() ,
,
可得![]() .
.
∴![]() .
.
②因为![]() ,所以以
,所以以![]() 为圆心,
为圆心,![]() 长为半径作圆与直线
长为半径作圆与直线![]() 一定有两个交点,当第一种情况成立时,必定存在一个与它互补的
一定有两个交点,当第一种情况成立时,必定存在一个与它互补的![]() .
.
可知:![]()
综上所述,这三个角之间的关系有两种,
![]() 或
或![]() .
.



 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 放在每个小正方形的边长为
放在每个小正方形的边长为![]() 的网格中,点
的网格中,点![]() 、
、![]() 、
、![]() 均落在格点上.
均落在格点上.
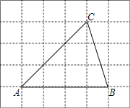
(1)![]() 的面积等于________;
的面积等于________;
![]() 若四边形
若四边形![]() 是
是![]() 中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明)________.
中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明)________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是瑞安部分街道示意图,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为“公交汽车”停靠点,甲公共汽车从
为“公交汽车”停靠点,甲公共汽车从![]() 站出发,按照
站出发,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的顺序到达
的顺序到达![]() 站,乙公共汽车从
站,乙公共汽车从![]() 站出发,按照
站出发,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的顺序到达
的顺序到达![]() 站,如果甲、乙两车分别从
站,如果甲、乙两车分别从![]() 、
、![]() 两站同时出发,各站耽误的时间相同,两辆车速度也一样,则( )
两站同时出发,各站耽误的时间相同,两辆车速度也一样,则( )
A. 甲车先到达指定站 B. 乙车先到达指定站
C. 同时到达指定站 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt直角△ABC中,∠BAC=90°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,则下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
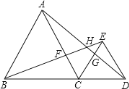
【题目】如图,点P、M、N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PV⊥AC于点N,若AB=12cm,求CM的长为______cm.
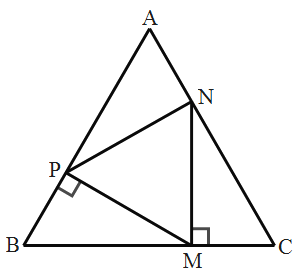
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八![]() 班组织了一次经典朗读比赛,甲、乙两队各
班组织了一次经典朗读比赛,甲、乙两队各![]() 人的比赛成绩如下表(
人的比赛成绩如下表(![]() 分制):
分制):
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
①甲队成绩的中位数是________分,乙队成绩的众数是________分;
②计算乙队的平均成绩和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com