
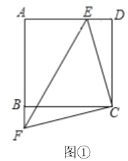
【题目】如图①,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点(点
边上的一动点(点![]() 与
与![]() 、
、![]() 点不重合),四边形
点不重合),四边形![]() 沿
沿![]() 折叠得边形
折叠得边形![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
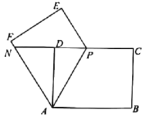
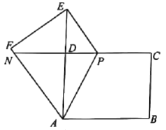
图① 图②
(1)求证:![]() ;
;
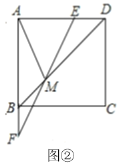
(2)如图②,若点![]() 恰好在
恰好在![]() 的延长线上时,试求出
的延长线上时,试求出![]() 的长度;
的长度;
(3)当![]() 时,求证:
时,求证:![]() 是等腰三角形.
是等腰三角形.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)由矩形的性质和平行线的性质得出∠BAP=∠APN,由折叠的性质得:∠BAP=∠PAN,得出∠APN=∠PAN,即可得出NA=NP;
(2)由矩形的性质得出CD=AB=4,AD=BC=3,∠BAD=∠B=∠ADC=90°,由折叠的性质得:AF=AB=4,EF=CB=3,∠F=∠B=90°,PE=PC,由勾股定理得出AE=![]() =5,求出DE=AE-AD=2,设DP=x,则PE=PC=4-x,在Rt△PDE中,由勾股定理得出方程,解方程即可;
=5,求出DE=AE-AD=2,设DP=x,则PE=PC=4-x,在Rt△PDE中,由勾股定理得出方程,解方程即可;
(3)过点D作GH∥AF,交EF于G,交AP于H,则GH∥AF∥PE,证出△PDH是等边三角形,得出DH=PH,∠ADH=∠PHD-∠PAD=30°=∠PAD,证出DH=AH,得出AH=PH,由平行线分线段成比例定理得出![]() ,得出EG=FG,再由线段垂直平分线的性质得出DE=DF即可.
,得出EG=FG,再由线段垂直平分线的性质得出DE=DF即可.
(1)证明;∵四边形ABCD是矩形,
∴AB∥CD,
∴∠BAP=∠APN,
由折叠的性质得:∠BAP=∠PAN,
∴∠APN=∠PAN,
∴NA=NP;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=4,AD=BC=3,∠BAD=∠B=∠ADC=90°,
∴∠PDE=90°,
由折叠的性质得:AF=AB=4,EF=CB=3,∠F=∠B=90°,PE=PC,
∴AE=![]() =5,
=5,
∴DE=AE-AD=2,
设DP=x,则PE=PC=4-x,
在Rt△PDE中,由勾股定理得:DP2+DE2=PE2,
即x2+22=(4-x)2,
解得:![]() ,即
,即![]() ;
;
(3)证明:过点D作GH∥AF,交EF于G,交AP于H,如图所示:
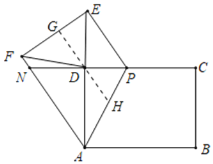
则GH∥AF∥PE,
∴∠PHD=∠NAH,
∵∠PAD=30°,
∴∠APD=90°-30°=60°,∠BAP=90°-30°=60°,
∴∠PAN=∠BAP=60°,
∴∠PHD=60°=∠APD,
∴△PDH是等边三角形,
∴DH=PH,∠ADH=∠PHD-∠PAD=30°=∠PAD,
∴DH=AH,
∴AH=PH,
∵GH∥AF∥PE,
∴![]() ,
,
∴EG=FG,
又∵GH⊥EF,
∴DE=DF,
∴△DEF是等腰三角形.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】在海洋上有一近似于四边形的岛屿,其平面如图甲,小明据此构造处该岛的一个数学模型(如图乙四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,AB=BC=5千米,CD=![]() 干米,AD=4
干米,AD=4![]() 干米.
干米.
(1)求小溪流AC的长.
(2)求四边形ABCD的面积.(结果保留根号)
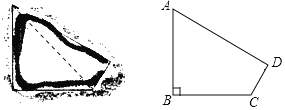
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形![]() 是正方形,点
是正方形,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() .
.
(1)如图①,连接![]() .求证:
.求证:![]() 是等腰直角三角形;
是等腰直角三角形;
(2)如图②,![]() 与
与![]() 交于点
交于点![]() ,若正方形
,若正方形![]() 的边长为6,
的边长为6,![]() ,求
,求![]() 的长.
的长.
(3)点![]() ,点
,点![]() 分别在边
分别在边![]() ,边
,边![]() 上,
上,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,若正方形
,若正方形![]() 的边长为6.
的边长为6.![]() 求
求![]() 的长(直接写出结果即可)
的长(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展“环境治理留住青山绿水,绿色发展赢得金山银山”活动,对其周边的环境污染进行综合治理.![]() 年对
年对![]() 、
、![]() 两区的空气量进行监测,将当月每天的空气污染指数(简称:
两区的空气量进行监测,将当月每天的空气污染指数(简称:![]() )的平均值作为每个月的空气污染指数,并将
)的平均值作为每个月的空气污染指数,并将![]() 年空气污染指数绘制如下表.据了解,空气污染指数
年空气污染指数绘制如下表.据了解,空气污染指数![]() 时,空气质量为优:
时,空气质量为优:![]() 空气污染指数
空气污染指数![]() 时,空气质量为良:
时,空气质量为良:![]() 空气污染指数
空气污染指数![]() 时,空气质量为轻微污染.
时,空气质量为轻微污染.
月份 地区 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出![]() 、
、![]() 两区的空气污染指数的平均数;
两区的空气污染指数的平均数;
(2)请从平均数、众数、中位数、方差等统计量中选两个对![]() 区、
区、![]() 区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
区的空气质量进行有效对比,说明哪一个地区的环境状况较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
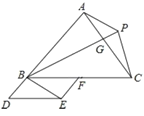
【题目】如图,点![]() 是
是![]() 的边
的边![]() 的延长线上一点,点
的延长线上一点,点![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合).以
重合).以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,又
,又![]() (点
(点![]() 、
、![]() 在直线
在直线![]() 的同侧),如果
的同侧),如果![]() ,那么
,那么![]() 的面积与
的面积与![]() 面积的比值为____________.
面积的比值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
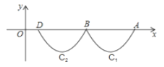
【题目】如图,抛物线 ![]() 与X轴交于点A、B,把抛物线在X轴及其下方的部分记作
与X轴交于点A、B,把抛物线在X轴及其下方的部分记作![]() ,将
,将![]() 向左平移得到
向左平移得到![]() ,
,![]() 与X轴交于点B、D,若直线
与X轴交于点B、D,若直线![]() 与
与![]() 、
、![]() 共有3个不同的交点,则m取值范围是( )
共有3个不同的交点,则m取值范围是( )
A. ![]() <m<
<m<![]() B.
B. ![]() <m<
<m<![]() C.
C. ![]() <m<
<m<![]() D.
D. ![]() <m<
<m<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连结EF,则线段EF的长的最小值是( )
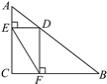
A.2.5B.2.4C.2.2D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com