
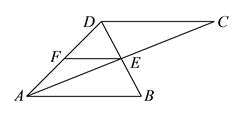
【题目】如图![]() ,
, ![]() 平分
平分![]() ,
, ![]() 平分
平分![]() ,
, ![]() 和
和![]() 交于点
交于点![]() ,
, ![]() 为
为![]() 的中点,连结
的中点,连结![]() .
.

(![]() )找出图中所有的等腰三角形.
)找出图中所有的等腰三角形.
(![]() )若
)若![]() ,
, ![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )所有的等腰三角形有:
)所有的等腰三角形有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(
;(![]() )
)![]() .
.
【解析】试题分析:
(1)由AB∥CD,AC平分∠BAD可得∠C=∠BAC=∠DAC,从而可得AD=CD,得到△ADC是等腰三角形;同理可△ABD是等腰三角形;证∠AED=90°,结合点F是AD中点,可得EF=FD=FA,从而可得△DEF和△AEF是等腰三角形;即图中共有4个等腰三角形;
(2)由∠AED=90°,AE=4,DE=3,由勾股定理可得AD=5,结合点F是AD中点,可得EF=![]() AD=2.5.
AD=2.5.
试题解析:
(![]() )图中等腰三角形共有4个,分别是:
)图中等腰三角形共有4个,分别是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .理由如下:
.理由如下:
∵AB∥CD,AC平分∠BAD,
∴∠C=∠BAC,∠BAC=∠DAC,
∴∠C=∠DAC,
∴AD=CD,
∴△ADC是等腰三角形;
同理可得:△ABD是等腰三角形;
∵BD平分∠ADC,AD=CD,
∴BD⊥AC,
∴∠AED=90°,
又∵点F是AD的中点,
∴EF=AF=DF,
∴△AEF和△DEF是等腰三角形;
综上所述,图中共有四个等腰三角形,分别是:△ADC、△ABD、△AEF和△DEF;
(![]() )∵∠AED=90°,AE=4,DE=3,
)∵∠AED=90°,AE=4,DE=3,
∴AD=![]() ,
,
又∵点F是AD的中点,
∴EF=![]() AD=
AD=![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】瑞士数学家欧拉是史上最伟大的四个数学家之一,目前在百度上搜索关键词“欧拉”,显示的搜索结果约为12 600 000条.将12 600 000用科学记数法表示应为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】健身运动已成为时尚,某公司计划组装![]() 、
、![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,捐给社区健身中心。组装一套
套,捐给社区健身中心。组装一套![]() 型健身器材需甲种部件
型健身器材需甲种部件![]() 个和乙种部件
个和乙种部件![]() 个,组装一套
个,组装一套![]() 型健身器材需甲种部件
型健身器材需甲种部件![]() 个和乙种部件
个和乙种部件![]() 个.公司现有甲种部件
个.公司现有甲种部件![]() 个,乙种部件
个,乙种部件![]() 个.
个.
(![]() )公司在组装
)公司在组装![]() 、
、![]() 两种型号的健身器材时,共有多少种组装方案?
两种型号的健身器材时,共有多少种组装方案?
(![]() )组装一套
)组装一套![]() 型健身器材需费用
型健身器材需费用![]() 元,组装一套
元,组装一套![]() 型健身器材需费用
型健身器材需费用![]() 元,求总组装费用最少的组装方案,并求出最少组装费用?
元,求总组装费用最少的组装方案,并求出最少组装费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级6个班举行毕业文艺汇演,每班3个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少6个.设舞蹈类节目有![]() 个.
个.
(1)用含![]() 的代数式表示:歌唱类节目有______________个;
的代数式表示:歌唱类节目有______________个;
(2)求九年级表演的歌唱类与舞蹈类节目数各有多少个?
(3)该校七、八年级有小品节目参与汇演,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计全场节目交接所用的时间总共16分钟.若从19:00开始,21:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.

解:∵FG//CD (已知)
∴∠2=_________(____________________________)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//__________(_____________________________)
∴∠B+________=180°(______________________________)
又∵∠B=50°
∴∠BDE=________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com