
 某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.
某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.分析 (1)将已知点的坐标代入一次函数的解析式,利用待定系数法确定其函数解析式即可;
(2)表示出有关总利润的二次函数的解析式,配方后即可确定最值;
(3)根据总利润等于1320万元列方程求解即可.
解答 解:(1)设y=kx+b,
则$\left\{\begin{array}{l}100k+b=20\\ 200k+b=10\end{array}\right.$,
解得$\left\{\begin{array}{l}k=-\frac{1}{10}\\ b=30\end{array}\right.$,
∴y与x的函数关系式为$y=-\frac{1}{10}x+30$(100≤x≤200);
(2)设公司去年获利w万元
则$w=(x-60)(-\frac{1}{10}x+30)-1200=-\frac{1}{10}{(x-180)^2}+240$,
∵$-\frac{1}{10}<0$,100≤x≤200,
∴当x=180时,w取最大值240,
∴去年获利最大为240万元;
(3)根据题意,得$(x-60)(-\frac{1}{10}x+30)+240=1320$,
解得x1=120,x2=240,
∵100≤x≤200,
∴x=120.
答:今年的产品售价定为120元/件时,可使去年和今年共获利1320万元.
点评 主要考查了二次函数在实际生活中的应用,弄懂题意,根据等量关系,列函数关系式,结合x的取值范围,可求得符合题意的x的值,其中要注意应该在自变量的取值范围内求得最大值.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | A | B | C | D |
| 时间t(h) | t<1 | 1≤t<2 | 2≤t<3 | t≥3 |
| 人数 | 5a | 5b | 5c | 5d |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
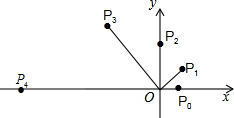 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…,则
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…,则查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 50 | 40 | 30 | 20 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
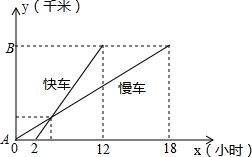 一慢车和一快车沿相同路线从A地到相距1200千米的B地,所行路程与时间的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到相距1200千米的B地,所行路程与时间的函数图象如图所示,试根据图象,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com