
【题目】如图,已知矩形![]() ,用直尺和圆规进行如下操作:
,用直尺和圆规进行如下操作:
①以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ;
;
②连接![]() ;
;
③以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ;
;
④连接![]() .
.
根据以上操作,解答下列问题:
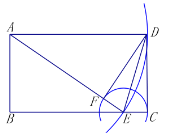
(1)线段![]() 与线段
与线段![]() 的位置关系是__________;
的位置关系是__________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)DF⊥AE;(2)17°
【解析】
(1)易证△DEF≌△DEC,得到∠DCE=∠DFE=90°,从而得到DF⊥AE;
(2)由△DEF≌△DEC得到∠FDE=∠CDE,所以∠FDC=2∠CDE=90°-![]() ,从而得到
,从而得到
![]() 的度数.
的度数.
解:(1)DF⊥AE,理由如下:
由题意:AD=AE
∴∠ADE=∠AED
又∵AD∥BC
∴∠ADE=∠DEC
∴∠AED=∠DEC
又∵EF=EC,ED=ED
∴△DEF≌△DEC(SAS)
∴∠DCE=∠DFE=90°
∴DF⊥AE;
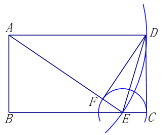
(2)由题意:AD=AE
∴∠ADE=∠AED
又∵AD∥BC
∴∠ADE=∠DEC
∴∠AED=∠DEC
又∵EF=EC,ED=ED
∴△DEF≌△DEC(SAS)
∴∠FDE=∠CDE
又∵∠ADF=56°
∴∠FDC=90°-56°=34°
∴∠CDE=17°


科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
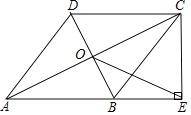
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把菱形![]() 向右平移至
向右平移至![]() 的位置,作
的位置,作![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() :④
:④![]() .
.
则其中所有成立的结论是( )
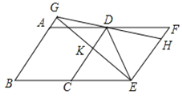
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
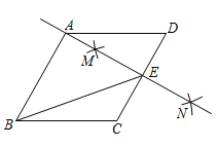
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
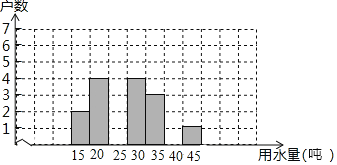
【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况::
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
(3)为了倡导“节约用水绿色环保”的意识,江赣市自来水公司实行“梯级用水、分类计费”,价格表如下:
月用水梯级标准 | Ⅰ级(30吨以内) | Ⅱ级(超过30吨的部分) |
单价(元/吨) | 2.4 | 4 |
如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在Ⅰ级标准?
(4)按上表收费,如果某用户本月交水费120元,请问该用户本月用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
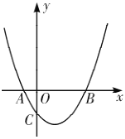
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称.
轴对称.
(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在直线![]() 下方的抛物线上是否存在一点
下方的抛物线上是否存在一点![]() ,使
,使![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com