解:第1个图形,菱形的个数为1,火柴棒的根数为4,
第2个图形,菱形的个数为5=2
2+1,火柴棒的根数为12=2×6=2×[2×(2+1)],
第3个图形,菱形的个数为14=3
2+2
2+1,火柴棒的根数为24=3×8=3×[2×(3+1)],
…
第n个图形,菱形的个数为n
2+…+3
2+2
2+1,火柴棒的根数为n[2(n+1)]=2n(n+1),
根据平方和求和公式:n
2+…+3
2+2
2+1=

n(n+1)(2n+1).
因此,菱形的个数的增长规律为:

n(n+1)(2n+1),
火柴棒的根数的增长规律2n(n+1).
分析:查出前三个图形所使用的火柴棒的根数与菱形的个数,根据数据的变化特点找出变化规律,然后写出第n个图形的菱形的个数的增长规律与火柴棒的增长规律即可.
点评:本题是对图形变化规律的考查,查出火柴棒的根数比较简单,难点在于查出菱形的个数,需要分单个的四根火柴棒组成的菱形与几个小菱形在一起组成的菱形,这是本题最容易出错的地方.

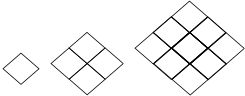 如图,用火柴棒摆菱形,请你通过观察探究:菱形的个数的增长规律与火柴棒的根数的增长规律.
如图,用火柴棒摆菱形,请你通过观察探究:菱形的个数的增长规律与火柴棒的根数的增长规律. n(n+1)(2n+1).
n(n+1)(2n+1). n(n+1)(2n+1),
n(n+1)(2n+1),
