
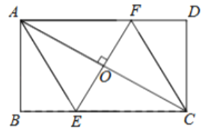
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=2,BC=4,求四边形AECF的面积.
【答案】(1)见解析;(2)5.
【解析】
(1)由四边形ABCD是矩形可以得到∠DAC=∠BCA ,过AC的中点0作EF⊥AC,由线段的垂直平分线可知AF=CF,AE=CE,则有∠DAC=∠FCA,等量代混得∠BCA=∠FCA,根据三角形的内角和可得∠OEC=∠OFC,根据等腰三角形性质和菱形的性质,即可得出四边形AECF菱形;
(2)由四边形AECF为菱形可得AE=EC,设AE=x,根据AB=2,BC=4和勾股定理可以求出AE,利用![]() 求出即可.
求出即可.
(1)证明:∵四边形ABCD是矩形
∴AD∥BC
∴∠DAC=∠BCA
又∵过AC的中点0作EF⊥AC
∴AF=CF,AE=CE
∴∠DAC=∠FCA
∴∠BCA=∠FCA,∠COE=90°
∴∠OEC=∠OFC
∴EC=FC
∴AF=CF=CE=AE
四边形AECF菱形
(2)由(1)得,四边形AECF为菱形
∴AE=EC
设AE=x,则BE=BC-EC=![]()
在RtΔABE中,![]()
即:![]()
解得,![]()
∴![]()
![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】下面是“作已知三角形的高”的尺规作图过程.
已知: ![]() .
.

求作: ![]() 边上的高
边上的高![]()
作法:如图,
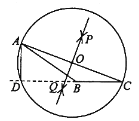
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
, ![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心, ![]() 为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
请回答;该尺规作图的依据是___________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
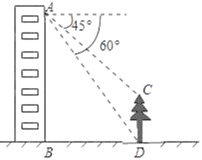
【题目】如图,小明在教学楼的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为10米.请你帮助小明计算树的高度(精确到0.1米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com