
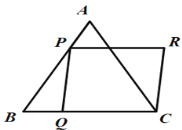
【题目】如图,等边△ABC边长为4,点P,Q分别是AB,BC边上的动点,且AP =BQ= x,作□PQCR,则用含x的代数式表示□PQCR的面积为______;当PC∥AR时, x =____.
【答案】![]() ;
; ![]() .
.
【解析】
过点P作PH⊥BC于点H,由AP=BQ=x得PB=QC=4-x,利用三角函数解Rt△BPH,得![]() ,进一步得到S与x的关系式.当PC∥AR时,证△AOR∽△ACOP,利用相似三角形对应边成比例列出方程求解即可.
,进一步得到S与x的关系式.当PC∥AR时,证△AOR∽△ACOP,利用相似三角形对应边成比例列出方程求解即可.
解:如图,过点P作PH⊥BC于点H,
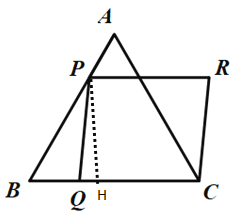
∴∠PHB=90°
∵等边三角形ABC
∴∠B=60°,BC=AB=4
∵AP=BQ=x,
∴PB=QC=4-x
在Rt△BPH中,∠B=60°
∴![]()
∴S平行四边形PQCR=QC·PH=![]() ;
;
当PC∥AR时,如图,连接PC,AR,AC、PR交于点O.
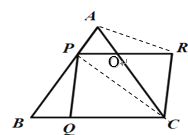
则△AOR∽△ACOP,
∴![]() =
=![]() ,
,
∵PR∥BC,
∴△APO是等边三角形,AO=AP=PO=x
∴OR=PR=PO=4-x-x=4-2x,CO=4-x
∴![]() =
=![]()
解得:x =![]()
∴当PC∥AR时, x =![]() .
.
故答案为:(1) ![]() ; (2)
; (2) ![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,开口向上的抛物线与![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为抛物线的顶点,
为抛物线的顶点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() . 若
. 若![]() 的长分别是方程
的长分别是方程![]() 的两根,且
的两根,且![]()
(1)求抛物线对应的二次函数解析式和点![]() 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
(3如图2,过点![]() 任作直线
任作直线![]() 交线段
交线段![]() 于点
于点![]() 求
求![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,请直接写出
,请直接写出![]() 的最大值.
的最大值.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
原题:如图1,点E,F分别在正方形ABCD的边BC,CD上,![]() ,连接EF,求证:EF=BE+DF.
,连接EF,求证:EF=BE+DF.
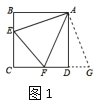
解题由于AB=AD,我们可以延长CD到点G,使DG=BE,易得![]() ,可证
,可证![]() .再证明
.再证明![]() ,得EF=FG=DG+FD=BE+DF.
,得EF=FG=DG+FD=BE+DF.
问题(1):如图2,在四边形ABCD中,AB=AD,![]() ,E,F分别是边BC,CD上的点,且
,E,F分别是边BC,CD上的点,且![]() ,求证:EF=BE+FD;
,求证:EF=BE+FD;

问题(2):如图3,在四边形ABCD中,![]() ,
,![]() ,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且
,AB=AD=1,点E,F分别在四边形ABCD的边BC,CD上的点,且![]() ,求此时
,求此时![]() 的周长
的周长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是杨辉三角系数表,它的作用是指导读者按规律写出行如(a+b)![]() 展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数。
展开式的系数,请你仔细观察下表中的规律,填出展开式中所缺的系数。
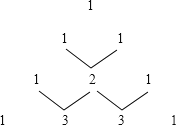
(1)、(a+b)=a+b
(2)、(a+b)![]() =a
=a![]() +2ab+b
+2ab+b![]()
(3)、(a+b) ![]() =a
=a![]() +3a
+3a![]() b+3ab
b+3ab![]() +b
+b![]()
(4)、(a+b)![]() =a
=a![]() + a
+ a![]() b+6a
b+6a![]() b
b![]() +4ab
+4ab![]() +b
+b![]()
(5)(a+b)![]() =a
=a![]() + a
+ a![]() b+ a
b+ a![]() b
b![]() + a
+ a![]() b
b![]() + ab
+ ab![]() +b
+b![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,AD是高,E,F分别是AB,AC中点,EF交AD于G,已知GF=1,AC= 6,△DEG的周长为10,则△ABC的周长为( )

A. 27-3![]() B. 28-3
B. 28-3![]() C. 28-4
C. 28-4![]() D. 29-5
D. 29-5![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将一副三角板(直角三角板![]() 和直角三角板
和直角三角板![]() )的两个顶点重合于点
)的两个顶点重合于点![]() .
.

(1)如图1,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,当
逆时针方向转动,当![]() 恰好平分
恰好平分![]() 时,
时,![]() 的度数是 _.
的度数是 _.
(2)如图2,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,如果三角板
,如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
(3)当三角板![]() 绕点
绕点![]() 继续转动到如图3所示的位置时,作射线
继续转动到如图3所示的位置时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() ,请你求出此时钝角
,请你求出此时钝角![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
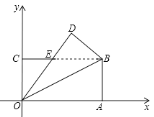
【题目】如图,矩形OABC的顶点与坐标原点O重合,将△OAB沿对角线OB所在的直线翻折,点A落在点D处,OD与BC相交于点E,已知OA=8,AB=4
(1)求证:△OBE是等腰三角形;
(2)求E点的坐标;
(3)坐标平面内是否存在一点P,使得以B,D,E,P为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A,B,C三点对应的数a,b,c满足(a+40)2+|b+10|=0,B为线段AC的中点.

(1)直接写出A,B,C对应的数a,b,c的值.
(2)如图1,点D表示的数为10,点P,Q分别从A,D同时出发匀速相向运动,点P的速度为6个单位/秒,点Q的速度为1个单位/秒.当点P运动到C后迅速以原速返回到A又折返向C点运动;点Q运动至B点后停止运动,同时P点也停止运动.求在此运动过程中P,Q两点相遇点在数轴上对应的数.
(3)如图2,M,N为A,C之间两点(点M在N左边,且它们不与A,C重合),E,F分别为AN,CM的中点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com