
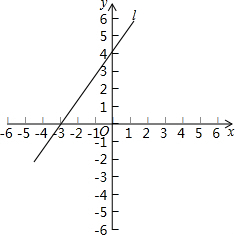 如图直线与两坐标轴的交点坐标分别是A(-3,0),B(0,4),O是坐标系原点:
如图直线与两坐标轴的交点坐标分别是A(-3,0),B(0,4),O是坐标系原点:分析 (1)设出函数解析式,将两点代入,运用待定系数法求解;
(2)C点的位置比较多,每个坐标轴上有三个点,依次寻找即可.
解答 解:(1)设函数解析式为y=kx+b,
两点代入得:$\left\{\begin{array}{l}{-3k+b=0}\\{b=4}\end{array}\right.$,
解得:k=$\frac{4}{3}$,b=4,
∴函数解析式为:y=$\frac{4}{3}$x+4;
(2)AB为腰的等腰三角形交坐标轴与C点,C点可以有6个值
C点坐标分别为(3,0),(-8,0),(0,9),(0,-1),(0,-4),(2,0).
点评 本题考查待定系数法求函数解析式及关于y轴对称的点的坐标的特点,难度不大,注意掌握待定系数法的运用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:
元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -3 | -2 | 1 | 2 | 3 | 4 | … |
| y | … | 12 | 5 | -4 | -3 | 0 | 5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com