
����Ŀ�����壺��P�ǡ�ABC�ڲ�����ϵĵ㣨������⣩���ڡ�PAB����PBC����PCA�У���������һ�����������ABC���ƣ���Ƶ�P�ǡ�ABC�������Ƶ㣮
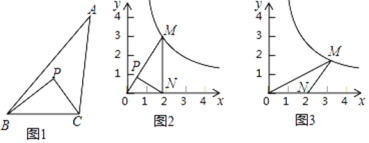
���磺��ͼ1����P�ڡ�ABC���ڲ�����PBC=��A����PCB=��ABC�����BCP�ס�ABC���ʵ�P�ǡ�ABC�������Ƶ㣮
����������ѧ֪ʶ������������ϣ�����������⣺
��ƽ��ֱ������ϵ�У���M������y=![]() ��x��0���ϵ�����һ�㣬��N��x���������ϵ�����һ�㣮
��x��0���ϵ�����һ�㣬��N��x���������ϵ�����һ�㣮
��1����ͼ2����P��OM��һ�㣬��ONP=��M����˵����P�ǡ�MON�������Ƶ㣻����M�������ǣ�![]() ��3������N�������ǣ�
��3������N�������ǣ�![]() ��0��ʱ�����P�����ꣻ
��0��ʱ�����P�����ꣻ
��2����ͼ3������M�������ǣ�3��![]() ������N�������ǣ�2��0��ʱ�����MON�������Ƶ�����ꣻ
������N�������ǣ�2��0��ʱ�����MON�������Ƶ�����ꣻ
��3���Ƿ���ڵ�M�͵�N��ʹ��MON�������Ƶ㣿�����ڣ���ֱ��д������������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��P��![]() ��
��![]() ������2����1��
������2����1��![]() ����2��
����2��![]() ������3������, M��
������3������, M��![]() ��3����N��
��3����N��![]() ��0����
��0����
��������
���⣨1������ONP=��M����NOP=��MON���ó���NOP�ס�MON��֤����P����MON�������Ƶ�����P��PD��x����D����tan��POD=![]() =
=![]() �������AON=60�㣬�ɵ�M��N������ó���MNO=90�㣬�����������ε����ʵó���NPO=��MNO=90�㣬��Rt��OPN���������Ǻ������OP=
�������AON=60�㣬�ɵ�M��N������ó���MNO=90�㣬�����������ε����ʵó���NPO=��MNO=90�㣬��Rt��OPN���������Ǻ������OP=![]() ��OD=
��OD=![]() ��PD=
��PD=![]() �����ɵó�����
�����ɵó�����
��2����MH��x����H���ɹ��ɶ������OM=![]() ��ֱ��OM�Ľ���ʽΪy=
��ֱ��OM�Ľ���ʽΪy=![]() x��ON=2����MOH=30�㣬���������������PQ��x����Q�������Ƶ�����ʵó�PO=PN��OQ=
x��ON=2����MOH=30�㣬���������������PQ��x����Q�������Ƶ�����ʵó�PO=PN��OQ=![]() ON=1�����P�������꼴����
ON=1�����P�������꼴����
�����MN=![]() =2�������������ε����ʵó�
=2�������������ε����ʵó�![]() �����PN=
�����PN=![]() �������P�ĺ����꼴����
�������P�ĺ����꼴����
��3��֤��OM=![]() =ON����MON=60�㣬�ó���MON�ǵȱ����������ɵ�P����MON���ڲ����ó���PON�١�OMN����PNO�١�MON�����ɵó�������
=ON����MON=60�㣬�ó���MON�ǵȱ����������ɵ�P����MON���ڲ����ó���PON�١�OMN����PNO�١�MON�����ɵó�������
����������⣺��1���ߡ�ONP=��M����NOP=��MON�����NOP�ס�MON������P����MON�������Ƶ���
��P��PD��x����D����tan��POD=![]() =
=![]() �����MON=60�㣮������M�������ǣ�
�����MON=60�㣮������M�������ǣ�![]() ��3������N�������ǣ�
��3������N�������ǣ�![]() ��0�������MNO=90�㣮�ߡ�NOP�ס�MON�����NPO=��MNO=90�㣮��Rt��OPN����OP=ONcos60��=
��0�������MNO=90�㣮�ߡ�NOP�ס�MON�����NPO=��MNO=90�㣮��Rt��OPN����OP=ONcos60��=![]() ����OD=OPcos60��=
����OD=OPcos60��=![]() =
=![]() ��PD=OPsin60��=
��PD=OPsin60��=![]() ��
��![]() =
=![]() ����P��
����P��![]() ��
��![]() ����
����
��2����MH��x����H����ͼ3��ʾ������M�������ǣ�3��![]() ������N�������ǣ�2��0������OM=
������N�������ǣ�2��0������OM=![]() =
=![]() ��ֱ��OM�Ľ���ʽΪy=
��ֱ��OM�Ľ���ʽΪy=![]() x��ON=2����MOH=30�㣬�����������
x��ON=2����MOH=30�㣬�����������
����ͼ3��ʾ����P����MON�����Ƶ������PON�ס�NOM��
��PQ��x����Q����PO=PN��OQ=![]() ON=1����P�ĺ�����Ϊ1����y=
ON=1����P�ĺ�����Ϊ1����y=![]() ��1=
��1=![]() ����P��1��
����P��1��![]() ����
����
����ͼ4��ʾ���ɹ��ɶ�������MN=![]() =2����P����MON�����Ƶ������PNM�ס�NOM����
=2����P����MON�����Ƶ������PNM�ס�NOM����![]() ����
����![]() �������PN=
�������PN=![]() ����P��������Ϊ
����P��������Ϊ![]() ������y=
������y=![]() x������
x������![]() =
=![]() x�������x=2����P��2��
x�������x=2����P��2��![]() ����
����
������������MON�������Ƶ������Ϊ��1��![]() ����2��
����2��![]() ����
����
��3�����ڵ�M�͵�N��ʹ��MON�������Ƶ���M��![]() ��3����N��
��3����N��![]() ��0��������������
��0��������������
��M��![]() ��3����N��
��3����N��![]() ��0������OM=
��0������OM=![]() =ON����MON=60�㣬���MON�ǵȱ�������������P����MON���ڲ������PON�١�OMN����PNO�١�MON�������ڵ�M�͵�N��ʹ��MON�������Ƶ���
=ON����MON=60�㣬���MON�ǵȱ�������������P����MON���ڲ������PON�١�OMN����PNO�١�MON�������ڵ�M�͵�N��ʹ��MON�������Ƶ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��һ��أ������ϱ�ʾ��m����n������֮��ľ������![]() .�����ʾ��a��
.�����ʾ��a��![]() ������֮��ľ�����5����ô
������֮��ľ�����5����ô![]() __________��
__________��
��2���������ϱ�ʾ��a�ĵ�λ��![]() ��6֮�䣬��
��6֮�䣬��![]() ��ֵ��
��ֵ��
��3����aȡ��ֵʱ��![]() ��ֵ��С����Сֵ�Ƕ��٣���˵������.
��ֵ��С����Сֵ�Ƕ��٣���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڼ䣬ij�̳��ƻ������ס���������Ʒ����֪��������Ʒ2��������Ʒ3������270Ԫ����������Ʒ3��������Ʒ2������230Ԫ��
��1����ס���������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳���������Ʒ��ÿ��40Ԫ���ۣ�����Ʒ��ÿ��90Ԫ���ۣ�Ϊ�����г������蹺���ס���������Ʒ��100�����Ҽ�����Ʒ������������������Ʒ������4������������������Ľ�����������ȷ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ����������⣺�߹���ͼ������֪�ǵĽ�ƽ���ߣ���֪����ͼ����BAC����������BAC�Ľ�ƽ����AP��
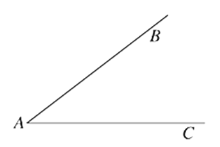
С�����������£�
��1����ͼ����ƽ������ȡһ��O��
��2���Ե�OΪԲ�ģ�AOΪ�뾶��Բ��������AB�ڵ�D��������AC�ڵ�E��
��3������DE������O������OP��ֱ���߶�DE������O�ڵ�P��
��4������P������AP��
��������AP����
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������OP![]() DE
DE
�� ![]() =______��________________________���������������ݣ���
=______��________________________���������������ݣ���
���BAP=______ ��________________________���������������ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B��C��������O����ֱ��BDƽ�֡�ABC������D��DE��AB����BC�ڵ�E����BC���ӳ�����ȡһ��F��ʹ��EF![]() DE��
DE��
��1����֤��DF�ǡ�O��������
��2������AF��DE�ڵ�M���� AD![]() 4��DE
4��DE![]() 5����DM�ij���
5����DM�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪��a��![]() ��2��b��
��2��b��![]() +2�������ʽa2b��ab2��ֵ��
+2�������ʽa2b��ab2��ֵ��
��2����֪ʵ��x��y����x2+10x+![]() +25��0����x+y��2019��ֵ�Ƕ��٣�
+25��0����x+y��2019��ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y1=��2x2+2��ֱ��y2=2x+2����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M=y1=y2�����磺��x=1ʱ��y1=0��y2=4��y1��y2����ʱM=0�������жϣ�
�ٵ�x��0ʱ��y1��y2�� �ڵ�x��0ʱ��xֵԽ��MֵԽС��
��ʹ��M����2��xֵ�����ڣ� ��ʹ��M=1��xֵ��![]() ��
��![]() ��
��
������ȷ���ǣ�������

����A���٢ڡ���B���٢ܡ���C���ڢۡ���D���ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪BD����ABC�Ľ�ƽ���ߣ�ED��BC����BAC=90������C=30����

��1����֤��CE=BE��
��2����AD=3������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��1��-1����B��2��3������PΪx����һ�㣬��|PA-PB|��ֵ���ʱ����P������Ϊ���������� ��
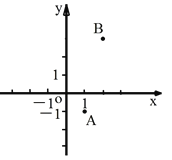
A.��-1��0��B.��![]() ��0��C.��
��0��C.��![]() ��0��D.��1��0��
��0��D.��1��0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com