
【题目】![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 为线段
为线段![]() 上一点(
上一点(![]() 点不和
点不和![]() 两点重合),连接
两点重合),连接![]() 并延长
并延长![]() ,在
,在![]() 的延长线上找一点
的延长线上找一点![]() ,使
,使![]() .点
.点![]() 为线段
为线段![]() 上一点(
上一点(![]() 点不和
点不和![]() 两点重合),连接
两点重合),连接![]() ,交
,交![]() 于点
于点![]() .
.
(1)如图1,若![]() 是线段
是线段![]() 的中点,求
的中点,求![]() .
.
(2)如图2,若点![]() 是线段
是线段![]() 的中点,
的中点,![]() ,求证:
,求证:![]() .
.

【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据等腰直角三角形的性质得到![]() ,根据勾股定理得到
,根据勾股定理得到![]() 根据线段的中点的定义得到
根据线段的中点的定义得到![]() ,由勾股定理得到结论;
,由勾股定理得到结论;
(2)过A作AH∥CD交BD于H,得到∠AHD=∠CDH,根据全等三角形的性质得到DE=EH,AH=CD,推出四边形AHCD是矩形,得到∠HAD=90°,根据全等三角形的性质得到BH=CF,由线段的和差得到结论.
解:(1)∵△ABC是等腰直角三角形,![]()
![]()
∵AD⊥CD,
∴∠ADC=90°,
∵CD=1,
∴![]()
∵F是线段AD的中点,
∴![]()
![]()
(2)过A作AH∥CD交BD于H,
∴∠AHD=∠CDH,
∵点E是线段AC中点,
∴AE=CE,
在△AEH与△CED中,
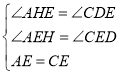
∴△AEH≌△CED(AAS),
∴DE=EH,AE=CE,
∴四边形AHCD是平行四边形,
∵∠ADC=90°,
∴四边形AHCD是矩形,
∴∠HAD=90°,
∵∠BAC=90°,
∴∠BAH=∠FAC,
∵DE⊥CF,
∴∠DFG=∠CDG,
∴∠AHE=∠DFG,
∴∠AHB=∠AFC,
在△ABH与△ACF中
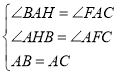
∴△ABH≌△ACF(AAS),
∴BH=CF,
∵BE=BH+EH,
∴CF+DE=BE.



科目:初中数学 来源: 题型:
【题目】某商店第一次用3000元购进某款书包,很快卖完,第二次又用2400元购进该款书包,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个.
(1)求第一次每个书包的进价是多少元?
(2)若第二次进货后按80元/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包按同一标准一次性打折销售,但要求这次的利润不少于480元,问最低可打几折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家用电器开发公司研制出一种新型电子产品,每件的生产成本为![]() 元,按定价
元,按定价![]() 元出售,每月可销售
元出售,每月可销售![]() 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价
万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价![]() 元,月销售量可增加
元,月销售量可增加![]() 万件.
万件.
(1)求出月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的函数关系式(不必写
(元)之间的函数关系式(不必写![]() 的取值范围);
的取值范围);
(2)求出月销售利润![]() (万元)(利润
(万元)(利润![]() 售价-成本价)与销售单价
售价-成本价)与销售单价![]() (元)之间的函数关系式(不必写
(元)之间的函数关系式(不必写![]() 的取值范围);
的取值范围);
(3)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于![]() 万元.
万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
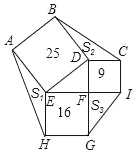
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
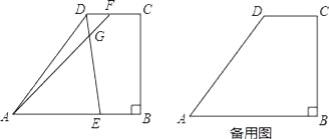
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DB∥AC,且DB=![]() AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,反比例函数y=![]() (x>0)的图象经过点A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连接AD,DC,CB.
(x>0)的图象经过点A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连接AD,DC,CB.
(1)求k的值;
(2)求证:DC∥AB;
(3)当AD∥BC时,求直线AB的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列游戏对双方公平的是( )
A. 随意转动被等分成![]() 个扇形,且分别均匀涂有红、黄、绿三种颜色的转盘,若指针指向绿色区域,则小明胜,否则小亮胜
个扇形,且分别均匀涂有红、黄、绿三种颜色的转盘,若指针指向绿色区域,则小明胜,否则小亮胜
B. 从一个装有![]() 个红球,
个红球,![]() 个黄球和
个黄球和![]() 个黑球(这些球除颜色外完全相同)的袋中任意摸出一个球,若是红球,则小明胜,否则小亮胜
个黑球(这些球除颜色外完全相同)的袋中任意摸出一个球,若是红球,则小明胜,否则小亮胜
C. 投掷一枚均匀的正方体形状的骰子,若偶数点朝上,则小明胜,若是奇数点朝上,则小亮胜
D. 从分别标有数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五张纸条中,任意抽取一张,若抽到的纸条所标的数字为偶数,则小明胜,若抽到的纸条所标的数字为奇数,则小亮胜
的五张纸条中,任意抽取一张,若抽到的纸条所标的数字为偶数,则小明胜,若抽到的纸条所标的数字为奇数,则小亮胜
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com