

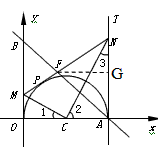
| 解(1)∵AT⊥AO,OM⊥AO,AO是⊙C的直径, ∴AT、OM是⊙C的切线, 又∵MN切⊙C于点P, ∴∠CMN= 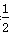 ∠OMN,∠CNM= ∠OMN,∠CNM=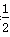 ∠ANM, ∠ANM,∵OM∥AN, ∴∠ANM+∠OMN=180°, ∴∠CMN+∠CNM = 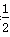 ∠OMN+ ∠OMN+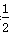 ∠ANM= ∠ANM=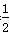 (∠OMN+ (∠OMN+ ∠ANM )=90°, ∠ANM )=90°, ∴∠CMN=90°; (2)由(1)可知:∠1+∠2 = 90 °,而∠2 +∠3=90°, ∴∠1 =∠3; ∴Rt△MOC∽Rt△CAN, ∴ 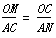 , ,∵直线y=-m(x-4)交x轴于点A,交y轴于点B, ∴A(4,0), ∴AC=CO=2, ∵OM=x,AN=y, ∵ 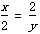 , ,∴y= 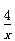 ; ;(3)∵OM=1, ∴AN=y= 4, 此时S四边形ANMO=10, ∵直线AB平分梯形ANMO的面积, ∴△ANF的面积为5, 过点F作FG⊥AN于G,则FG·AN=5, ∴FG=, ∴点F的横坐标为4- 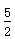 = =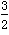 , ,∵M(0,1),N(4,4), ∴直线MN的解析式为y= 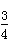 x+1, x+1,∵F点在直线MN上, ∴F点的纵坐标为y= 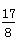 , ,∴ F( 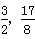 ) ) ∵点F又在直线y=-m(x-4)上 ∴ 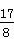 =-m( =-m(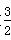 -4) -4)∴m= 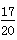 。 。 |
 |


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线l1:y=
如图,已知直线l1:y=| 2 |
| 3 |
| 8 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com