
【题目】小明准备给长![]() 米,宽
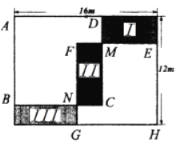
米,宽![]() 米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形
米的长方形空地栽种花卉和草坪,图中I、II、III三个区域分别栽种甲、乙、丙三种花卉,其余区域栽种草坪.四边形![]() 和
和![]() 均为正方形,且各有两边与长方形边重合;矩形
均为正方形,且各有两边与长方形边重合;矩形![]() (区域II)是这两个正方形的重叠部分,如图所示.
(区域II)是这两个正方形的重叠部分,如图所示.
(1)若花卉均价为![]() 元
元![]() ,种植花卉的面积为
,种植花卉的面积为![]()
![]() ,草坪均价为
,草坪均价为![]() 元
元![]() ,且花卉和草坪栽种总价不超过
,且花卉和草坪栽种总价不超过![]() 元,求
元,求![]() 的最大值.
的最大值.
(2)若矩形![]() 满足
满足![]() .
.
①求![]() ,
,![]() 的长.
的长.
②若甲、乙、丙三种花卉单价分别为![]() 元
元![]() ,
,![]() 元
元![]() ,
,![]() 元
元![]() ,且边
,且边![]() 的长不小于边
的长不小于边![]() 长的
长的![]() 倍.求图中I、II、III三个区域栽种花卉总价
倍.求图中I、II、III三个区域栽种花卉总价![]() 的最大值.
的最大值.
【答案】(1)![]() 的最大值为52米2;(2)①MF的长为4米,FN的长为8米;②
的最大值为52米2;(2)①MF的长为4米,FN的长为8米;②![]() 的最大值为
的最大值为![]() 元.
元.
【解析】
(1)先求出长方形空地的面积,从而可得栽种草坪的面积,再根据“总价不超过![]() 元”建立一元一次不等式,然后求解即可得;
元”建立一元一次不等式,然后求解即可得;
(2)①设![]() ,
,![]() ,根据正方形的性质、线段的和差可得MF、FN的长,再根据
,根据正方形的性质、线段的和差可得MF、FN的长,再根据![]() 可得a、b的关系等式,由此即可得出答案;
可得a、b的关系等式,由此即可得出答案;
②先在①的基础上,求出W关于a的函数表达式,再根据题意求出a的取值范围,然后利用二次函数的性质求解即可得.
(1)长方形空地的面积为![]() (米2)
(米2)
由题意得:![]()
解得![]()
故![]() 的最大值为52米2;
的最大值为52米2;
(2)①设![]() ,
,![]()
![]() 四边形
四边形![]() 和
和![]() 均为正方形
均为正方形
![]() ,
,![]()
![]() ,
,![]()
又![]()
![]()
解得![]()
![]() (米),
(米),![]() (米)
(米)
答:MF的长为4米,FN的长为8米;
②由①可知,![]() ,即
,即![]()
![]()
![]()
![]()
![]()
则由题意得:![]()
![]()
又![]() 且
且![]()
![]() 且
且![]()
解得![]()
由二次函数的性质可知,当![]() 时,
时,![]() 随a的增大而减小
随a的增大而减小
则当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() (元)
(元)
答:图中I、II、III三个区域栽种花卉总价![]() 的最大值为7040元.
的最大值为7040元.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
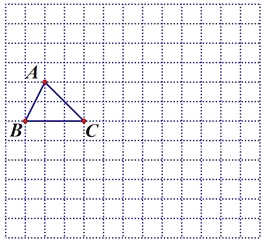
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度后得到△A1B1C1.画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2.画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.我市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如图不完整的统计图.
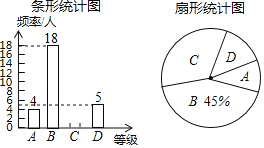
根据所给信息,解答以下问题:
(1)本次抽样调查抽取了 名学生的成绩;在扇形统计图中,D对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
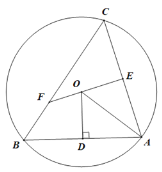
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解班级学生数学课前预习的具体情况,郑老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(2)扇形统计图中“课前预习不达标”对应的圆心角度数是 ;
(3)为了共同进步,郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为___________米(精确到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BC,垂足为E,若BD=![]() ,BC=6,则AB=( )
,BC=6,则AB=( )

A.![]() B.2C.
B.2C.![]() D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com