
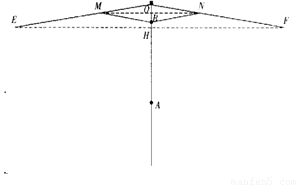
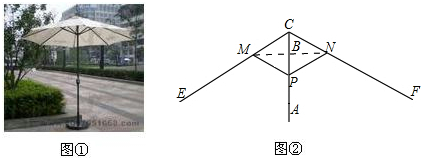
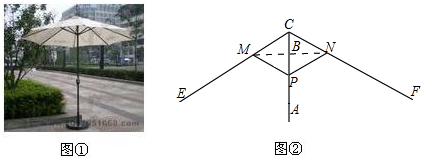
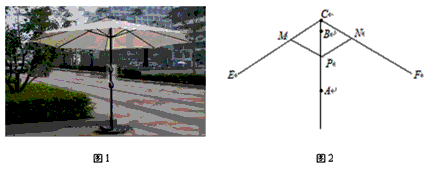
图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点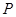 与点
与点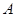 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点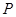 由
由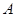 向
向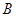 移动;当点
移动;当点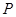 到过点
到过点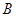 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有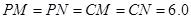 分米,
分米,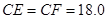 分米,
分米,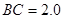 分米
分米

(1)求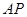 长的取值范围; (2)当
长的取值范围; (2)当 时,求
时,求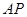 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为 (结果保留
(结果保留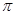 ).
).
(1)0≤ ≤10. (2)6(3)
≤10. (2)6(3)
【解析】(1)∵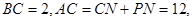
∴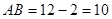
∴ 的取值范围为:0≤
的取值范围为:0≤ ≤10. ····················· 1分
≤10. ····················· 1分
(2)∵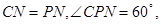 ∴
∴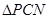 等边三角形. ∴
等边三角形. ∴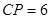 .
.
∴ .
.
即当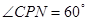 时,
时, 分米. ······················ 2分
分米. ······················ 2分
(3)伞张得最开时,点 与点
与点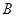 重合.
重合.
连接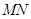 ,
,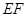 .分别交
.分别交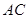 于
于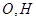
∵ ,
,
∴四边形为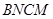 菱形,
菱形,
∴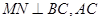 是
是 的平分线,
的平分线,
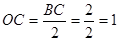 .
.
在Rt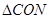 中
中
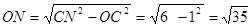 .
.
∵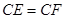 ,
,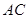 是
是 的平分线,
的平分线,
∴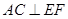 .
.
∴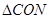 ~
~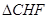 .
.
∴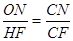 .∴
.∴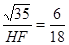 。
。
∴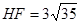 .
.
∴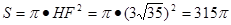 (平方分米). ·············· 5分
(平方分米). ·············· 5分
(1)根据题意,得AC=CN+PN,进一步求得AB的长,即可求得AP的取值范围;
(2)根据等边三角形的判定和性质即可求解;
(3)连接MN、EF,分别交AC于B、H.此题根据菱形CMPN的性质求得MB的长,再根据相似三角形的对应边的比相等,求得圆的半径即可.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年江西抚州市崇仁四中初三第二次月考数学试卷(带解析) 题型:解答题
图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点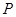 与点
与点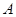 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点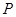 由
由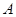 向
向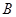 移动;当点
移动;当点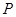 到过点
到过点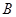 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有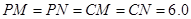 分米,
分米,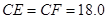 分米,
分米,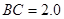 分米
分米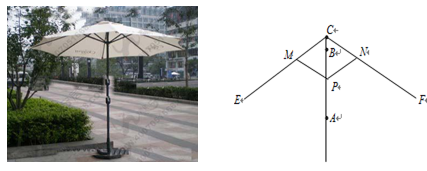
(1)求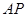 长的取值范围; (2)当
长的取值范围; (2)当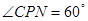 时,求
时,求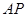 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为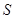 (结果保留
(结果保留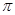 ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com