
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位) 
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(﹣1,0)和点B,与反比例函数y= ![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n). 
(1)求k的值;
(2)求反比例函数的解析式;
(3)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y= ![]() 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )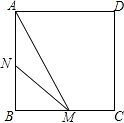
A.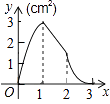
B.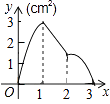
C.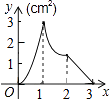
D.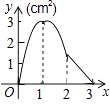
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒 ![]() 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).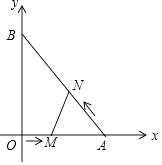
(1)当t=3秒时,直接写出点N的坐标;
(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;
(3)当t为何值时,△MNA是一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α. 
(1)用含α的式子表示h(不必指出α的取值范围);
(2)当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com