
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴正半轴于点
轴正半轴于点![]() .
.
(1)如图1,当![]() 时.
时.
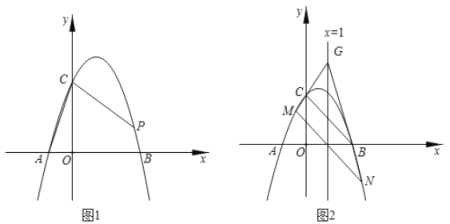
①直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
②若抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
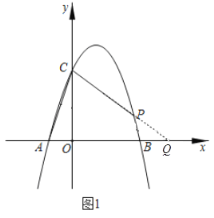
(2)如图2,平移直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 在定直线
在定直线![]() 上运动,求
上运动,求![]() 的值.
的值.
【答案】(1)①![]() ,
,![]() ,
,![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)①令x=0,可求点C坐标,令y=0,可求A点,B点坐标;
②延长CP交x轴于点E,由勾股定理和等腰三角形的性质可求点Q坐标,再求直线CE的解析式,联立方程可求点P坐标;(2)先求出BC解析式,再求出点M,N的横坐标,最后利用联立![]() 可解决问题.
可解决问题.
(1)①当m=3时,y=-x2+2x+3,
当x=0时,y=3,则点C(0,3),
当y=0时,0=-x2+2x+3,
∴x1=3,x2=-1,
∴![]() ,
,![]() ,
,![]() ;
;
②如图1,延长![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
联立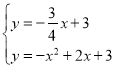 ,
,
∴![]() ,
,
∴![]() (舍),
(舍),![]()
∵![]() 在抛物线上,
在抛物线上,
∴![]() ;
;
(2)如图2,
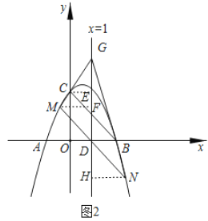
令![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
设![]() 解析式为:
解析式为:![]() ,
,
联立![]() ,即
,即 ![]() ,
,
∴![]() ,
,
同理:设![]() 解析式为:
解析式为:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 的解析式为
的解析式为![]() ,
,
∴设![]() 解析式为:
解析式为:![]() ,
,
联立![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 即
即![]() ,
,
联立![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】一个小球沿着足够长的光滑斜面向上滚动,它的速度与时间满足一次函数关系,其部分数据如下表:

(1) 求小球的速度v与时间t的关系.
(2)小球在运动过程中,离出发点的距离S与v的关系满足![]() ,求S与t的关系式,并求出小球经过多长时间距离出发点32m?
,求S与t的关系式,并求出小球经过多长时间距离出发点32m?
(3)求时间为多少时小球离出发点最远,最远距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.
(1)连接ED,若CD=3,AE=4,求AB的长;
(2)如图2,若点F为AD的中点,连接EB、CF,求证:CF⊥EB.
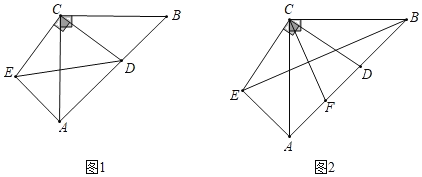
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 为圆O的直径, PQ切圆O于T , AC⊥PQ于C ,交圆O于 D .
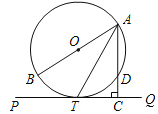
(1)求证: AT 平分∠BAC ;
(2)若 AD =2 , TC=![]() ,求圆O的半径.
,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法.下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.问题情境:在四边形ABCD中,AC是对角线,E为边BC上一点,连接AE.以E为旋转中心,将线段AE顺时针旋转,旋转角与∠B相等,得到线段EF,连接CF.
(1)特例如图1,若四边形ABCD是正方形,求证:AC⊥CF;
(2)拓展分析一:如图2,若四边形ABCD是菱形,探究下列问题:
①当∠B=50°时,求∠ACF的度数;
②针对图2的条件,写出一般的结论(不必证明);
(3)拓展探究二:如图3,若四边形ABCD是矩形,且BC=kAB(k>1).若前提条件不变,特例分析中得到的结论还成立吗?若成立,请证明;若不成立,修改题中的条件使结论成立(不必证明).
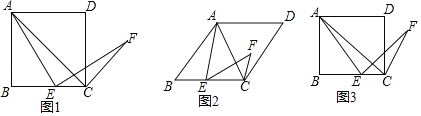
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨某中学学校为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类).根据图中提供的信息,解答下面的问题:

(1)在这次调查中,参与问卷调查的学生共有多少名学生?
(2)通过计算补全条形统计图;
(3)若学校有900名学生,估计喜欢篮球和足球的学生共有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
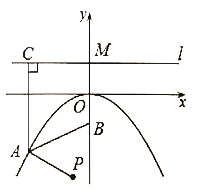
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com