
【题目】骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的![]() 型车去年6月份销售总额为3.2万元,今年经过改造升级后
型车去年6月份销售总额为3.2万元,今年经过改造升级后![]() 型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的
型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的![]() 型车数量相同,则今年6月份
型车数量相同,则今年6月份![]() 型车销售总额将比去年6月份销售总额增加
型车销售总额将比去年6月份销售总额增加![]() .
.
![]() ,
,![]() 两种型号车的进货和销售价格表:
两种型号车的进货和销售价格表:
|
| |
进货价格(元 | 1100 | 1400 |
销售价格(元 | 今年的销售价格 | 2400 |
(1)求今年6月份![]() 型车每辆销售价多少元;
型车每辆销售价多少元;
(2)该车行计划7月份新进一批![]() 型车和
型车和![]() 型车共50辆,且
型车共50辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,应如何进货才能使这批车获利最多?
型车数量的两倍,应如何进货才能使这批车获利最多?
【答案】(1)2000元;(2)![]() 型车17辆,
型车17辆,![]() 型车33辆
型车33辆
【解析】
(1)设去年6月份![]() 型车每辆销售价
型车每辆销售价![]() 元,那么今年6月份
元,那么今年6月份![]() 型车每辆销售
型车每辆销售![]() 元,根据销售总额和每辆销售价列出方程,即可解决问题.
元,根据销售总额和每辆销售价列出方程,即可解决问题.
(2)设今年7月份进![]() 型车
型车![]() 辆,则
辆,则![]() 型车
型车![]() 辆,获得的总利润为
辆,获得的总利润为![]() 元,先求出
元,先求出![]() 的范围,构建一次函数,利用函数性质解决问题.
的范围,构建一次函数,利用函数性质解决问题.
解:(1)设去年6月份![]() 型车每辆销售价
型车每辆销售价![]() 元,那么今年6月份
元,那么今年6月份![]() 型车每辆销售
型车每辆销售![]() 元,
元,
根据题意得![]() ,
,
解得:![]() ,
,
经检验,![]() 是方程的解.
是方程的解.
![]() 时,
时,![]() .
.
答:今年6月份![]() 型车每辆销售价2000元.
型车每辆销售价2000元.
(2)设今年7月份进![]() 型车
型车![]() 辆,则
辆,则![]() 型车
型车![]() 辆,获得的总利润为
辆,获得的总利润为![]() 元,
元,
根据题意得![]() ,
,
解得:![]() ,
,
![]() ,
,
![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 当
当![]() 时,可以获得最大利润.
时,可以获得最大利润.
答:进货方案是![]() 型车17辆,
型车17辆,![]() 型车33辆.
型车33辆.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知Rt△AOB的两条直角边0A、08分别在y轴和x轴上,并且OA、OB的长分别是方程x2—7x+12=0的两根(OA<0B),动点P从点A开始在线段AO上以每秒l个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
(1)求A、B两点的坐标。
(2)求当t为何值时,△APQ与△AOB相似,并直接写出此时点Q的坐标.
(3)当t=2时,在坐标平面内,是否存在点M,使以A、P、Q、M为顶点的四边形是平行四边形?若存在,请直接写出M点的坐标;若不存在,请说明理由.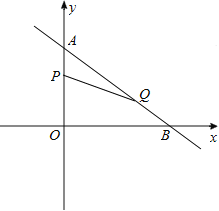
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有四张标着数字 ![]() ,
,![]() ,
,![]() ,
,![]() 的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
的卡片,这些卡片除数字外都相同.甲同学按照一定的规则抽出两张卡片,并把卡片上的数字相加.下图是他所画的树状图的一部分.
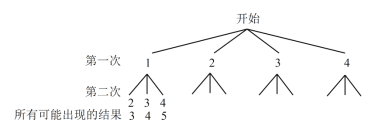
(1)由上图分析,甲同学的游戏规则是:从袋子中随机抽出一张卡片后 (填"放回"或"不放回"),再随机抽出一张卡片;
(2)帮甲同学完成树状图;
(3)求甲同学两次抽到的数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]()
![]() ,并且
,并且![]() 满足
满足![]() .一动点
.一动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动;动点
移动;动点![]() 从点
从点![]() 出发在线段
出发在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,点
运动,点![]() 分别从点
分别从点![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() (秒)
(秒)

(1)求![]() 两点的坐标;
两点的坐标;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形?并求出此时
是平行四边形?并求出此时![]() 两点的坐标.
两点的坐标.
(3)当![]() 为何值时,
为何值时,![]() 是以
是以![]() 为腰的等腰三角形?并求出此时
为腰的等腰三角形?并求出此时![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
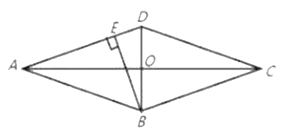
【题目】如图,在菱形ABCD中,![]() 、
、![]() 、
、![]() 分别是菱形ABCD的两条对角线长和边长,这时我们把关于
分别是菱形ABCD的两条对角线长和边长,这时我们把关于![]() 的形如“
的形如“![]() ”的一元二次方程称为“菱系一元二次方程”.请解决下列问题:
”的一元二次方程称为“菱系一元二次方程”.请解决下列问题:
(1)填空:①当![]() ,
,![]() 时,
时,![]() .
.
②用含![]() ,
,![]() 的代数式表示
的代数式表示![]() 值,
值,![]() .
.
(2)求证:关于![]() 的“菱系一元二次方程”
的“菱系一元二次方程”![]() 必有实数根;
必有实数根;
(3)若![]() 是“菱系一元二次方程”
是“菱系一元二次方程”![]() 的一个根,且菱形的面积是25,BE是菱形ABCD的AD边上的高,求BE的值.
的一个根,且菱形的面积是25,BE是菱形ABCD的AD边上的高,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=![]() 的图象上,则k的值为( )
的图象上,则k的值为( )

A.-4 B.4 C.-2 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-4(k-1)x+4k2=0有两个实数根x1、x2
(1) 求k的取值范围
(2) 若x1x2-2|x1+x2|=4,求k的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com