解:(1)DC=

CM
如图二,连接DM并延长DM交BC于N,
∵∠EDA=∠ABC=90°,
∴DE∥BC,
∴∠DEM=∠MCB,
∵在△EMD和△CMN中,
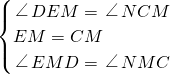
,
∴△EMD≌△CMN(ASA),
∴CN=DE=DA,MN=MD
∵BA=BC,
∴BD=BN,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,∠DBM=

∠DBN=45°=∠BDM,
∴△BMD为等腰直角三角形.
∴DC=

CM;
(2)DC=

CM,
理由:如图三,连接DM,作CN∥DE交DM的延长线于N,连接BN,
∴∠E=∠MCN=45°.
∵点M是BE的中点,
∴EM=CM.
∵在△EMD和△CMN中,

∴△EMD≌△CMN(ASA),
∴CN=DE=DA,MN=MD,
∵∠DAE=∠BAC=∠ACB=45°,
∴∠DAB=∠NCB=90°
∵在△DBA和△NBC中
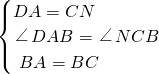
,
∴△DBA≌△NBC(SAS),
∴∠DBA=∠NBC,DB=BN,
∴∠DBN=∠ABC=90°,
∴△DBN是等腰直角三角形,且BM是底边的中线,
∴BM⊥DM,∠DBM=

∠DBN=45°=∠BDM,
∴△BMD为等腰直角三角形.
∴DC=

CM.
分析:(1)延长DM交BC于N,根据平行线的性质和判定推出∠DEM=∠MCB,根据ASA推出△EMD≌△CMN,证出CN=AD即可;
(2)作CN∥DE交DM的延长线于N,连接BN,根据平行线的性质求出∠E=∠NCM,根据ASA证△DBA≌△NBC,推出△DBN是等腰直角三角形,根据等腰直角三角形的性质即可推出△BMD为等腰直角三角形.
点评:本题综合考查了等腰直角三角形,等腰三角形的性质和判定,平行线的性质和判定,全等三角形的性质和判定,此题综合性比较强,培养了学生分析问题和解决问题的能力,类比思想的运用,题型较好,难度较大.

 CM.将△ADE绕点A逆时针旋转,当点D在AC上(如图二)或当点E在BA的延长线上(如图三)时,请你猜想DC与CM有怎样的数量关系,并选择一种情况加以证明.
CM.将△ADE绕点A逆时针旋转,当点D在AC上(如图二)或当点E在BA的延长线上(如图三)时,请你猜想DC与CM有怎样的数量关系,并选择一种情况加以证明.
 CM
CM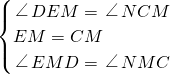 ,
, ∠DBN=45°=∠BDM,
∠DBN=45°=∠BDM, CM;
CM; CM,
CM,

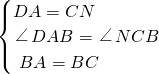 ,
, ∠DBN=45°=∠BDM,
∠DBN=45°=∠BDM, CM.
CM.

 阅读快车系列答案
阅读快车系列答案

