
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=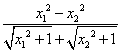 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
科目:初中数学 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=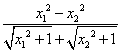 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
查看答案和解析>>
科目:初中数学 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=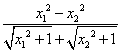 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
查看答案和解析>>
科目:初中数学 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
= -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
查看答案和解析>>
科目:初中数学 来源: 题型:
【例3】 设函数f(x)= ![]() -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
= -a(x1-x2)
-a(x1-x2)
=(x1-x2)(![]() -a).
-a).
(1)当a≥1时,∵![]() <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=![]() ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中![]() <1利用了
<1利用了![]() >|x1|≥x1,
>|x1|≥x1, ![]() >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com