
【题目】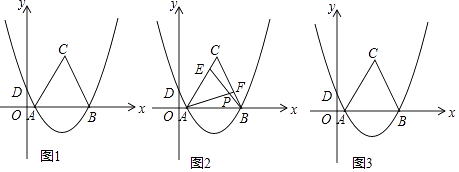
如图1,抛物线y=ax2+bx+ ![]() ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM= ![]() S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).
【答案】
(1)解:将点A(1,0),B(7,0)代入抛物线的解析式得: 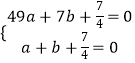 ,
,
解得:a= ![]() ,b=﹣2.
,b=﹣2.
∴抛物线的解析式为y= ![]() x2﹣2x+
x2﹣2x+ ![]() .
.
(2)解:存在点M,使得S△ABM= ![]() S△ABC.
S△ABC.
理由:如图所示:过点C作CK⊥x轴,垂足为K.
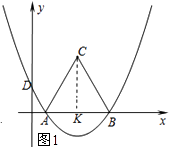
∵△ABC为等边三角形,
∴AB=BC=AC=6,∠ACB=60°.
∵CK⊥AB,
∴KA=BK=3,∠ACK=30°.
∴CK=3 ![]() .
.
∴S△ABC= ![]() ABCK=
ABCK= ![]() ×6×3=9
×6×3=9 ![]() .
.
∴S△ABM= ![]() ×9
×9 ![]() =12.
=12.
设M(a, ![]() a2﹣2a+
a2﹣2a+ ![]() ).
).
∴ ![]() AB|y|=12,即
AB|y|=12,即 ![]() ×6×(
×6×( ![]() a2﹣2a+
a2﹣2a+ ![]() )=12,
)=12,
解得:a1=9,a2=﹣1.
∴点M的坐标为(9,4)或(﹣1,4).
(3)解:①结论:AF=BE,∠APB=120°.
∵△ABC为等边三角形,
∴BC=AB,∠C=∠ABF.
∵在△BEC和△AFB中 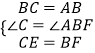 ,
,
∴△BEC≌△AFB.
∴AF=BE,∠CBE=∠BAF.
∴∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°.
∴∠APB=180°﹣60°=120°.
②当AE≠BF时,由①可知点P在以M为圆心,在以AB为弦的圆上,过点M作MK⊥AB,垂足为k.
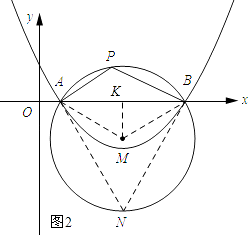
∵∠APB=120°,
∴∠N=60°.
∴∠AMB=120°.
又∵MK⊥AB,垂足为K,
∴AK=BK=3,∠AMK=60°.
∴AK=2 ![]() .
.
∴点P运动的路径= ![]() =
= ![]() .
.
当AE=BF时,点P在AB的垂直平分线上时,如图所示:过点C作CK⊥AB,则点P运动的路径=CK的长.
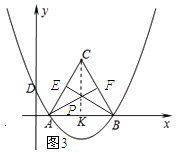
∵AC=6,∠CAK=60°,
∴KC=3 ![]() .
.
∴点P运动的路径为3 ![]() .
.
综上所述,点P运动的路径为3 ![]() 或
或 ![]() .
.
【解析】(1)将点A(1,0),B(7,0)代入抛物线的解析式得到关于a、b方程组,解关于a、b的方程组即可求得a、b的值;
(2)过点C作CK⊥x轴,垂足为K.依据等边三角形的性质可求得CK然后依据三角形的面积公式结合已知条件可求得S△ABM的面积,然后依据三角形的面积公式可得到关于a的方程,从而可得到点M的坐标;
(3)①首先证明△BEC≌△AFB,依据全等三角形的性质可知:AF=BE,∠CBE=∠BAF,然后通过等量代换可得∠FAB+∠ABP=∠ABP+∠CBE=∠ABC=60°,最后依据三角形的内角和定理可求得∠APB;
②当AE≠BF时,由①可知点P在以AB为直径的圆上,过点M作ME⊥AB,垂足为E.先求得⊙M的半径,然后依据弧长公式可求得点P运动的路径;当AE=BF时,点P在AB的垂直平分线上时,过点C作CK⊥AB,则点P运动的路径=CK的长.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右依次记为A1、A2、A3、…、An,已知第1个正方形中的一个顶点A1的坐标为(1,1),则点A2019的纵坐标为( )

A. 2019 B. 2018 C. 22018 D. 22019
查看答案和解析>>
科目:初中数学 来源: 题型:
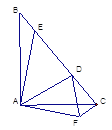
【题目】如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ABE绕点![]() 顺时针旋转90
顺时针旋转90![]() 后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△
后,得到△ACF,连接DF.下列结论中:①∠DAF=45° ②△![]() ≌△
≌△![]() ③AD平分∠EDF ④
③AD平分∠EDF ④![]() ;正确的有______________(填序号)
;正确的有______________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )

A. 65° B. 66° C. 70° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把(sinα)2记作sin2α,根据图1和图2完成下列各题.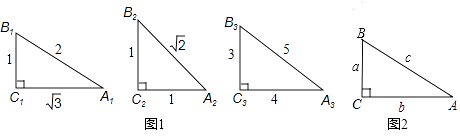
(1)sin2A1+cos2A1= , sin2A2+cos2A2= , sin2A3+cos2A3=;
(2)观察上述等式猜想:在Rt△ABC中,∠C=90°,总有sin2A+cos2A=;
(3)如图2,在Rt△ABC中证明(2)题中的猜想:
(4)已知在△ABC中,∠A+∠B=90°,且sinA= ![]() ,求cosA.
,求cosA.
查看答案和解析>>
科目:初中数学 来源: 题型:
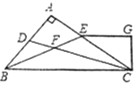
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG//BC,且![]() 于G,下列结论:①
于G,下列结论:①![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() ;其中正确的结论是( )
;其中正确的结论是( )
A.只有①③B.只有①③④C.只有②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )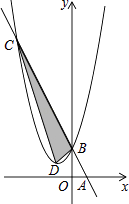
A.8:1
B.6:1
C.5:1
D.4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: ![]() ,求旗杆AB的高度(
,求旗杆AB的高度( ![]() ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com