
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
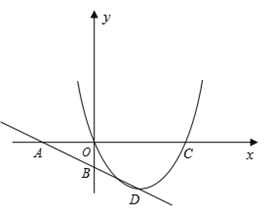
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
【答案】(1)![]() ;(2)点
;(2)点![]() ;(3)
;(3)![]() .
.
【解析】试题分析: ![]() 先求出点
先求出点![]() 的坐标,把点
的坐标,把点![]() 的坐标代入抛物线即可求出抛物线的解析式.
的坐标代入抛物线即可求出抛物线的解析式.
![]() 分两种情况进行讨论.
分两种情况进行讨论.
![]() 在
在![]() 中,用余弦得到
中,用余弦得到![]() 设
设![]() 根据勾股定理求出
根据勾股定理求出![]() 的值,求出点
的值,求出点![]() 的坐标,根据待定系数法求出直线的解析式.
的坐标,根据待定系数法求出直线的解析式.
试题解析:
(1)由题知:D点的横坐标为2,
∴![]() ,
,
![]() 把
把![]() 代入抛物线:
代入抛物线: ![]() 解之得:
解之得: 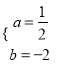
∴抛物线的解析式为: ![]()
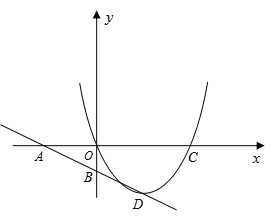
(2)存在点![]()
设对称轴与![]() 轴交于点
轴交于点![]() ,
, ![]()
易知: ![]()
![]()
情况1: ![]() 点在
点在![]() 点上方,则
点上方,则![]()
若![]() 则
则![]()
∴![]() 解得:
解得: ![]() ,
,
∴![]() .
.
若![]() 则
则![]()
![]() 解得:
解得: ![]()
∴ ![]() .
.
情况2:若P在D点的下方,则![]() 没有一个角会为
没有一个角会为![]()
∴![]() 与
与![]() 不可能相似
不可能相似
综上可知:存在点![]()
(3)、设![]() 与
与![]() 轴交于点
轴交于点![]() ,连NC交抛物线对称轴于一点,即为圆心M点,
,连NC交抛物线对称轴于一点,即为圆心M点,

![]()
在![]() 中,
中, ![]()
![]() 设
设![]()
则: 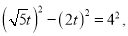 解得:
解得: ![]()
![]() ∴点
∴点![]() 坐标为(0,8),
坐标为(0,8),
![]()
设过点![]() 且与
且与![]() 相切的直线为
相切的直线为![]()
则![]() ,把
,把![]() 点代入有:
点代入有: ![]() ,解得:
,解得: ![]()
∴过点![]() 且与
且与![]() 相切的直线为
相切的直线为 ![]() .
.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了 5 千米到达小明家,继续向东走了 1.5 千米到达小红家,然后向西走了 9.5 千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1 个单位长度表示 1 千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点 A 表示,小红家用点 B 表示,小刚家用点 C 表示)
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油 0.6 升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上老师设计了一个数学游戏:若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”。甲、乙、丙、丁四位同学各有一张多项式卡片,下面是甲、乙、丙、丁四位同学的对话:
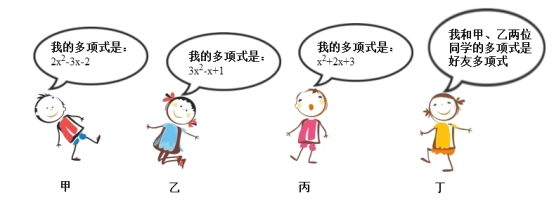
请根据对话解答下列问题:
(1)判断甲、乙、丙三位同学的多项式是否为“友好多项式”,并说明理由.
(2)丁的多项式是什么?(请直接写出所有答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华某天上午9时骑自行车离开家,17时回家,他有意描绘了离家的距离与时间的变化情况,如图所示.
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和11时,他分别离家多远?
(3)他最初到达离家最远的地方是什么时间?离家多远?
(4)11时到13时他行驶了多少千米?
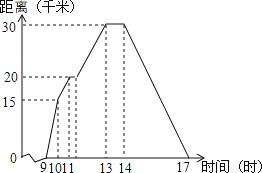
查看答案和解析>>
科目:初中数学 来源: 题型:
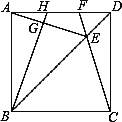
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com